The side BA and DC of a quadrilateral ABCD are produced to E and F respectively. If ∠BCF=a0,∠ABC=x∘,∠ADC=y∘and∠DAE=b∘,
prove thatx+y=a+b.

We have∠1+b∘=180∘======⇒∠1=(180∘−b∘)(linear pair)Also∠2+a∘=180∘(linear pair)======⇒∠A+∠B+∠C+∠D=360∘(sum of all the angles of a quadrilateral)======⇒(180−b)∘+x∘+(180−a)∘+y∘=360∘======⇒x+y=a+b
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
The sides BA and DC of a quadrilateral ABCD are produced as shown in Figure. Prove that a+b=x+y. Figure
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC~EDA.
View SolutionABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB = BE and AD = DF. Prove that : ΔBEC≅ΔDCF.
View SolutionIn the given figure BC is produced on both sides to points D and E respectively. Find the values of x and y
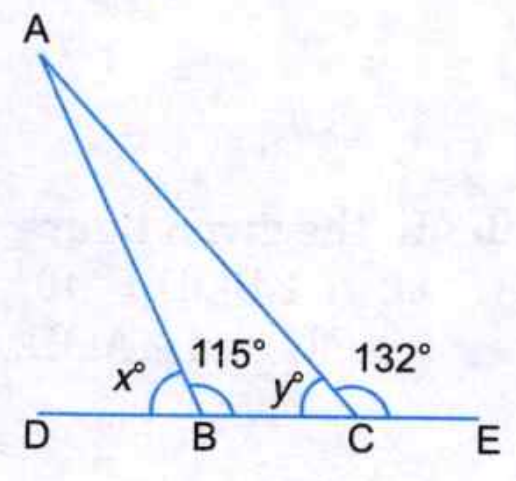
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionE si a point on side AD produced of a parallelogram ABCD and BE intersects DC at F. prove that △ABE~△CFB.
View SolutionABCD is a cyclic quadrilateral , Sides AB and DC produced meet at point E , whereas sides BC and AD produced meet at point F.
If ∠DCF:∠F:∠E=3:5:4 find the angles of the cyclic quadrilateral ABCD.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe equations of two equal sides ABandAC of an isosceles triangle ABC are x+y=5 and 7x−y=3 , respectively. Then the equation of side BC if ar(ABC)=5unit2 is x−3y+1=0 (b) x−3y−21=0 3x+y+2=0 (d) 3x+y−12=0
View Solution
