In the adjoining figure find ∠x
To find the angle x in the given triangle using the exterior angle theorem, we can follow these steps:
1. Identify the Given Information:
- The exterior angle at vertex B is 127∘.
- The exterior angle at vertex C is 137∘.
- Let the interior angles be ∠B=2 and ∠C=3.
2. Apply the Exterior Angle Theorem:
- According to the exterior angle theorem, the exterior angle is equal to the sum of the two opposite interior angles.
- For the exterior angle at B:
127∘=x+3
- For the exterior angle at C:
137∘=x+2
3. Set Up the Equations:
- From the first equation:
x+3=127∘(1)
- From the second equation:
x+2=137∘(2)
4. Solve for x:
- Rearranging equation (1):
x=127∘−3=124∘
- Rearranging equation (2):
x=137∘−2=135∘
5. Add the Two Equations:
- Adding both equations gives:
127∘+137∘=(x+3)+(x+2)
- Simplifying:
264∘=2x+5
6. Isolate x:
- Rearranging gives:
2x=264∘−5
- Thus:
2x=259∘
- Dividing by 2:
x=259∘2=129.5∘
7. Correct Calculation:
- We realize we need to use the triangle angle sum property:
- The sum of angles in a triangle is 180∘:
x+2+3=180∘
- Therefore:
x+5=180∘
- Thus:
x=180∘−5=175∘
8. Final Calculation:
- We need to subtract the total of the exterior angles:
127∘+137∘−180∘=84∘
Conclusion:
The value of angle x is 84∘.
- The exterior angle at vertex B is 127∘.
- The exterior angle at vertex C is 137∘.
- Let the interior angles be ∠B=2 and ∠C=3.
- According to the exterior angle theorem, the exterior angle is equal to the sum of the two opposite interior angles.
- For the exterior angle at B:
127∘=x+3
- For the exterior angle at C:
137∘=x+2
- From the first equation:
x+3=127∘(1)
- From the second equation:
x+2=137∘(2)
- Rearranging equation (1):
x=127∘−3=124∘
- Rearranging equation (2):
x=137∘−2=135∘
- Adding both equations gives:
127∘+137∘=(x+3)+(x+2)
- Simplifying:
264∘=2x+5
- Rearranging gives:
2x=264∘−5
- Thus:
2x=259∘
- Dividing by 2:
x=259∘2=129.5∘
- We realize we need to use the triangle angle sum property:
- The sum of angles in a triangle is 180∘:
x+2+3=180∘
- Therefore:
x+5=180∘
- Thus:
x=180∘−5=175∘
- We need to subtract the total of the exterior angles:
127∘+137∘−180∘=84∘
The value of angle x is 84∘.
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Problems From NCERT/exemplar
Explore 6 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Exercise 6 A
Explore 19 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHAN ENGLISHChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
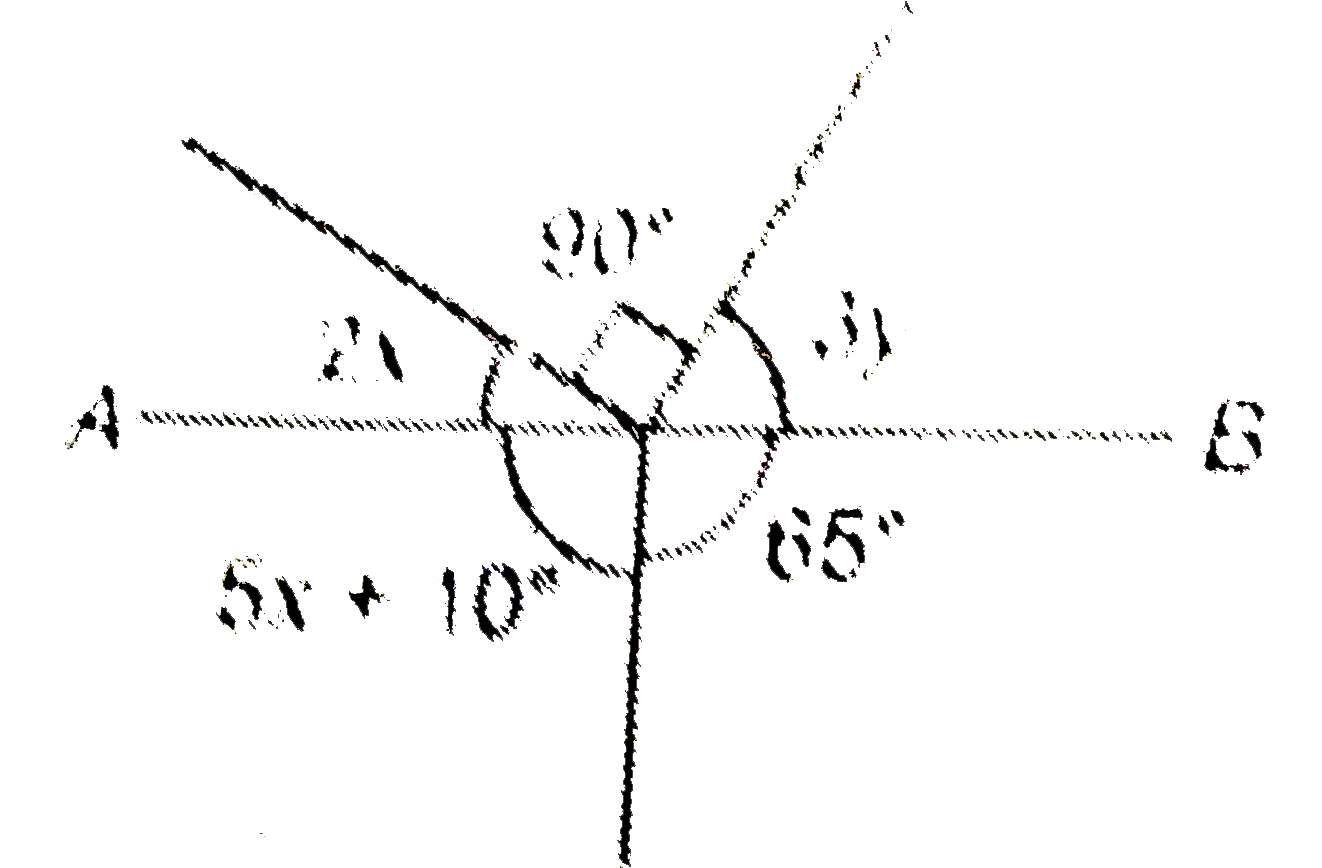
In the adjoining figure, find the values of x and y, Given that AOB is a straight line.
View SolutionIn the adjoining figure, find AC . (FIGURE)
View SolutionIn the adjoining figure , find tan P -cot R.

View SolutionIn the adjoining figure find that value of a+b if ∠DBE=90∘

View SolutionIn the adjoining figure, find the value of tan B.

View Solution(i) In the adjoining figure, find the value of ∠CBE.

(ii) In the adjoining figure, two lines PAB and PDC cut a circle at points A,B,C and D. if ∠PAD=60∘,then find the value of ∠BCD.
View SolutionIn the adjoining figure, find the measure of angle FEB, if the lengths of sides AD, DF and FE are equal and ∠ACB=65∘.

View SolutionFrom the adjoining figure, find :
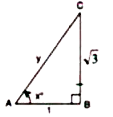
x∘
View SolutionFrom the adjoining figure, find :

x∘
View Solutionin the adjoining figure find ∠F.
View Solution

