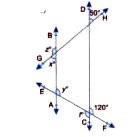
In the following figure , AB||CD . Find ∠PQR and reflex aangle PQR
To solve the problem of finding angle PQR and reflex angle PQR given that AB is parallel to CD, follow these steps:
1. Identify the Given Information:
- We have two parallel lines, AB and CD.
- We need to find angle PQR and its reflex angle.
2. Construct a Parallel Line:
- Draw a line EF that is parallel to both AB and CD. This helps in applying properties of parallel lines.
3. Label the Angles:
- Let angle APQ be 28 degrees.
- Let angle PQF be angle 1.
- Let angle QRF be angle 2.
4. Apply the Alternate Interior Angles Theorem:
- Since AB is parallel to EF and PQ is a transversal, we can say:
angle APQ=angle PQF(alternate interior angles)
Therefore, angle 1 (PQF) = 28 degrees.
5. Apply the Alternate Interior Angles Theorem Again:
- Now consider the parallel line EF and CD with PQ as the transversal:
angle PQF=angle QRF(alternate interior angles)
Therefore, angle 2 (QRF) = 38 degrees.
6. Calculate Angle PQR:
- Angle PQR can be expressed as the sum of angle 1 and angle 2:
angle PQR=angle 1+angle 2=28∘+38∘=66∘
7. Calculate Reflex Angle PQR:
- The reflex angle PQR is calculated as:
Reflex angle PQR=360∘−angle PQR=360∘−66∘=294∘
Final Answers:
- Angle PQR = 66 degrees
- Reflex angle PQR = 294 degrees
- We have two parallel lines, AB and CD.
- We need to find angle PQR and its reflex angle.
- Draw a line EF that is parallel to both AB and CD. This helps in applying properties of parallel lines.
- Let angle APQ be 28 degrees.
- Let angle PQF be angle 1.
- Let angle QRF be angle 2.
- Since AB is parallel to EF and PQ is a transversal, we can say:
angle APQ=angle PQF(alternate interior angles)
Therefore, angle 1 (PQF) = 28 degrees.
- Now consider the parallel line EF and CD with PQ as the transversal:
angle PQF=angle QRF(alternate interior angles)
Therefore, angle 2 (QRF) = 38 degrees.
- Angle PQR can be expressed as the sum of angle 1 and angle 2:
angle PQR=angle 1+angle 2=28∘+38∘=66∘
- The reflex angle PQR is calculated as:
Reflex angle PQR=360∘−angle PQR=360∘−66∘=294∘
- Angle PQR = 66 degrees
- Reflex angle PQR = 294 degrees
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Problems From NCERT/exemplar
6 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 A
19 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- NUMBER SYSTEMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
Similar Questions
Knowledge Check
In the given figure, AB∣∣CD. Find the value of x
 A20B25C40D60
A20B25C40D60
In the adjoining figure AB||CD, find x and y

View SolutionIn the given figure if AB|| CD find ∠APMandPQD
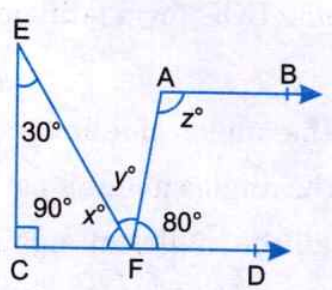
View SolutionIn the given figure, AB||CD||EF. Find x, y and z

View SolutionIn each of the following figures AB∣∣CD. Find the unknown angles, giving reasons
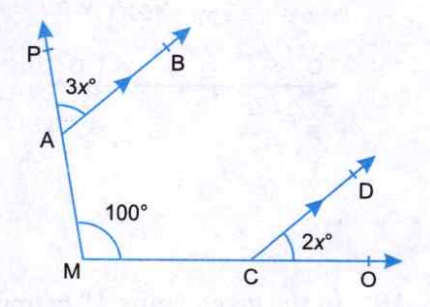
View SolutionIn each of the following figures AB∣∣CD. Find the unknown angles, giving reasons
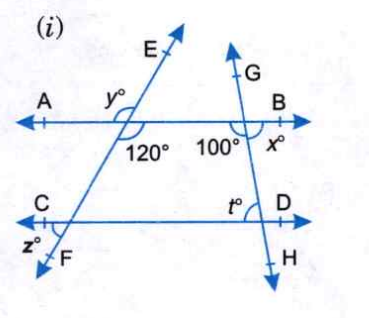
View SolutionIn the figure if AB || CD and AD||BC, find ∠Aand∠D
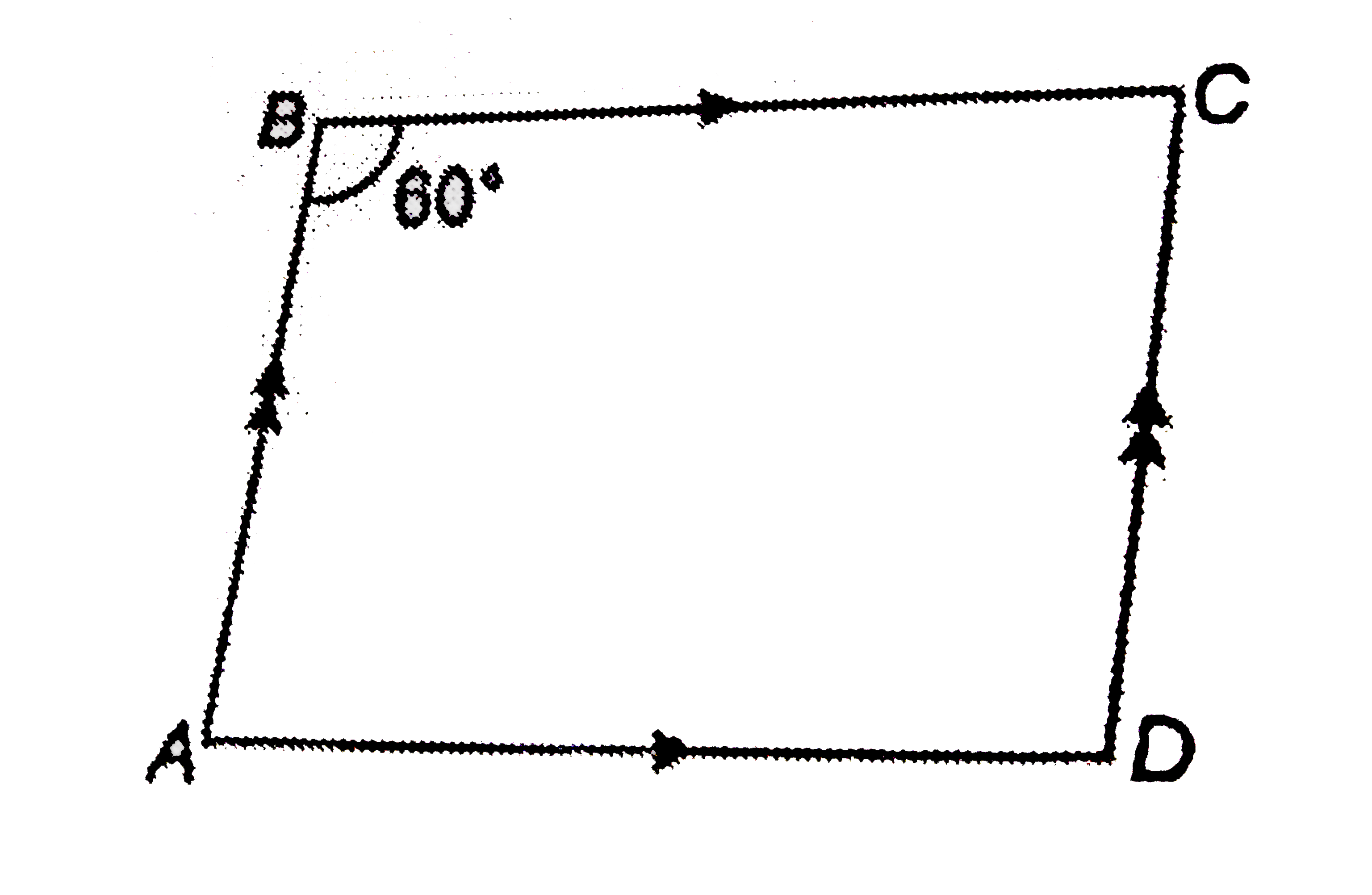
View SolutionIn each of the following figures, AB∣∣CD and EF is a transversal. Find the value of x in each case
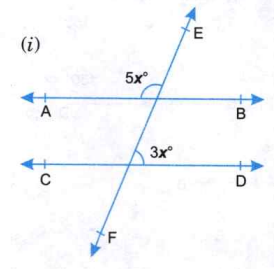
View Solution