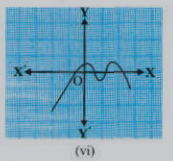
In general, given a polynomial pix) of degree n, the graph of y = p(x) intersects the x-axis at utmost n points. Therefore, a polynomial p(.r) of degree n has at most n zeroes:
 Solution in Punjabi
Solution in Punjabi
Step by step video & image solution for In general, given a polynomial pix) of degree n, the graph of y = p(x) intersects the x-axis at utmost n points. Therefore, a polynomial p(.r) of degree n has at most n zeroes: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Aftab tells his daughter, “Seven years ago, 1 was seven limes as old as you were then. Also, three years from now, 1 shall be three times as old as you will be." (Isn't this interesting?) Represent this situation algebraically and graphically.
View SolutionFind the probability of getting a head when a coin is tossed once. Also find the probability of getting a tail.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionComplete adjectant figure so that X-axis and Y-axis are the lines of symmetry of the completed figure.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View Solution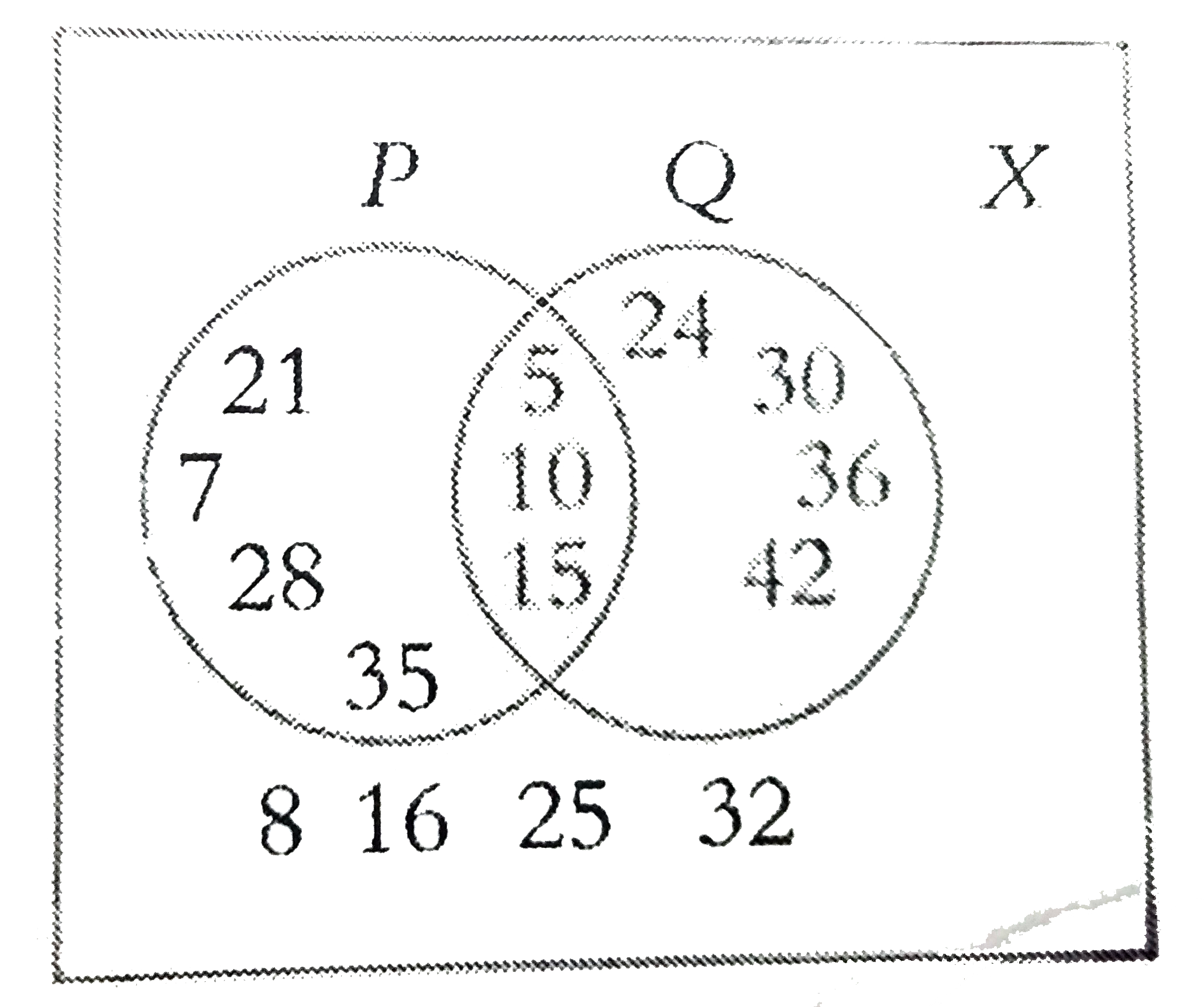
From the above Venn diagram ,find n(P-Q)+n(Q-p)=_____.
View Solution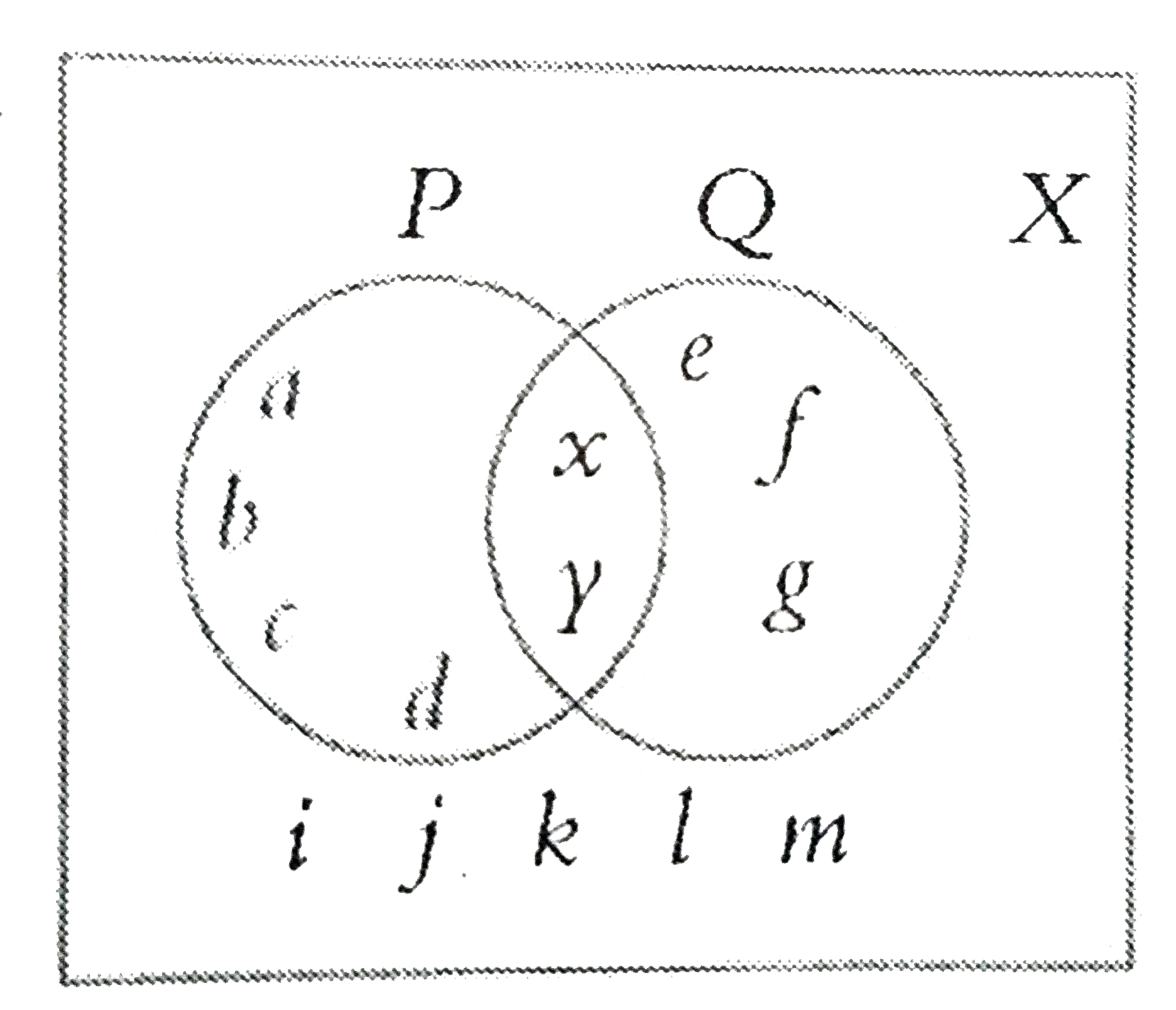
From the above Venn diagram ,Find n(P−Q)+n(Q−P)
View SolutionAt x=0, value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_024_Q01.png" width="80%"gt
View Solution
