In Fig.
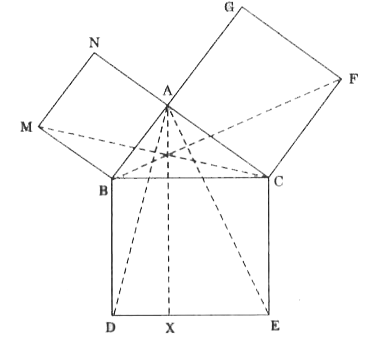
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX⊥DE meets BC at Y. Show that : ar(BYXD)=ar(ABMN).Solution in Punjabi
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX⊥DE meets BC at Y. Show that : ar(BYXD)=ar(ABMN).Solution in Punjabi
Step by step video & image solution for In Fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX _|_ DE meets BC at Y. Show that : ar(BYXD)=ar(ABMN). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
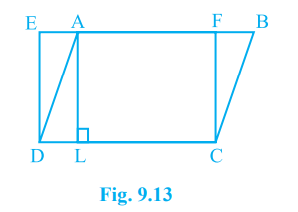
In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL
 View Solution
View SolutionGiven an arc of a circle, complete the circle.
 View Solution
View Solutionदी गए आकृति में ABC एक समकोण त्रिभुज है जिसके कोण A समकोण है | BCED,ACFG और ABMN क्रमशः भुजाओं BC ,CA और AB पर बने वर्ग है| रेखाखण्ड AX⊥DE भुजा BC से बिंदु Y पर मिलता हैं |दर्शाइए की :
(i)ΔMBC≡ΔABD
(ii)ar(BYXD)=2ar(MBC)
(iii)ar(BYXD)=ar(ABMN)
(iv) ΔFCB=ΔACE
(v)ar(CYXE)=2ar(FCB)
(vi)ar(CYXE)=ar(ACFG)
(vii)ar(BCED)=ar(ABMN)+ar(ACFG)
(viii)BC2=AB2+AC2
(##KCSHINMATIXC11SLV032_Q01##)08:36View SolutionIn the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX ⊥ DE meets BC at Y. Show that
(i) ti⟩MBC=ti⟩(MBC)
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ti⟩FCB=ti⟩ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
 05:33View Solution
05:33View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB espectively. Line segments AX bot DE meets BC at Y. and DE at X. Join AD, AE also BF and CM (See the figure). Show that (i) DeltaMBC ~=DeltaABD
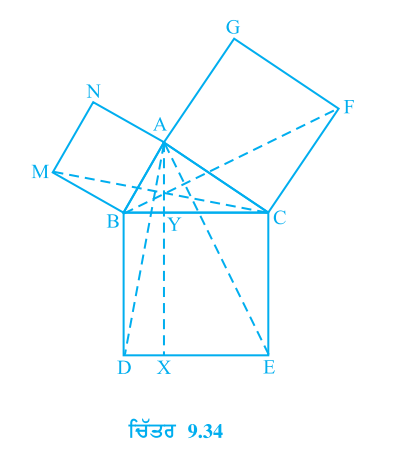
05:45View Solutionਚਿੱਤਰ 9.34 ਵਿੱਚ, ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ, ਜਿਸਦਾ ਕੋਣ A ਸਮਕੋਣ ਹੈ। BCED, ACFG ਅਤੇ ABMN ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ BC, CA ਅਤੇ AB ਉੱਤੇ ਬਣੇ ਵਰਗ ਹਨ। ਰੇਖਾ ਖੰਡ AX⊥DE ਭੁਜਾ ਨੂੰ ਬਿੰਦੂ Y 'ਤੇ ਮਿਲਦਾ ਹੈ। ਕਿ: △MBC≅△ABD
 06:23View Solution
06:23View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) =2 ar (MBC)
11:30View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) = ar (ABMN)
03:27View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BCED) =ar (ABMN) + ar (ACFG)
11:38View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: triangleMBC congtriangleABD
06:53View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BYXD) =2ar(MBC)
05:54View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BYXD) = ar(ABMN)
06:30View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: triangleFCB congtriangleACE
06:44View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(CYXE) = 2ar(FCB)
07:05View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(CYXE) = ar(ACFG)
04:04View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BCED) = ar(ABMN) + ar (ACFG)
03:59View Solution

