The side mirror of a scooter got broken. The mechanic replaced it with a plane mirror. Mention any inconvenience that the driver of the scooter will face while using it?

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the question about the inconvenience a driver of a scooter will face when using a plane mirror instead of a convex mirror, we can break down the solution into clear steps:
1. Understanding the Types of Mirrors:
- A plane mirror reflects light and produces an image that is the same size as the object but appears at the same distance behind the mirror as the object is in front of it.
- A convex mirror, on the other hand, is curved outward and allows for a wider field of view, making it possible to see more area behind the vehicle.
2. Identifying the Function of Side Mirrors:
- Side mirrors on vehicles, especially scooters, are designed to help the driver see vehicles and obstacles that are behind and to the sides of them. This is crucial for safe driving and changing lanes.
3. Inconvenience of Using a Plane Mirror:
- When a plane mirror is used instead of a convex mirror, the driver will face the inconvenience of having a limited field of view.
- The plane mirror will only show a narrow area directly behind the scooter, making it difficult for the driver to see vehicles or obstacles that are further away or to the sides.
4. Conclusion:
- The main inconvenience the driver will face is the inability to see the traffic spread over a larger area behind them. This could lead to potential accidents or unsafe maneuvers because the driver may not be aware of vehicles approaching from behind or the sides.
Final Answer:
The driver of the scooter will face the inconvenience of not being able to see the traffic spread over a large area behind them when using a plane mirror, as it provides a limited field of view compared to a convex mirror.
---

Updated on:18/9/2024

Class 7 PHYSICS LIGHT

Topper's Solved these Questions

Knowledge Check

A convex lens forms a real image of a point object at a distance of 50 cm from the convex lens. A concave lens is placed 10 cm behind the convex lens on the image side. On placing a plane mirror on the image side and facing the concave lens, it is observed that the final image now coincides with the object itself. The focal length of the concave lens is
A50 cm
B20 cm
C40 cm
D25 cm
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $∣ ∣ ψ^{2} ∣ ∣$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.

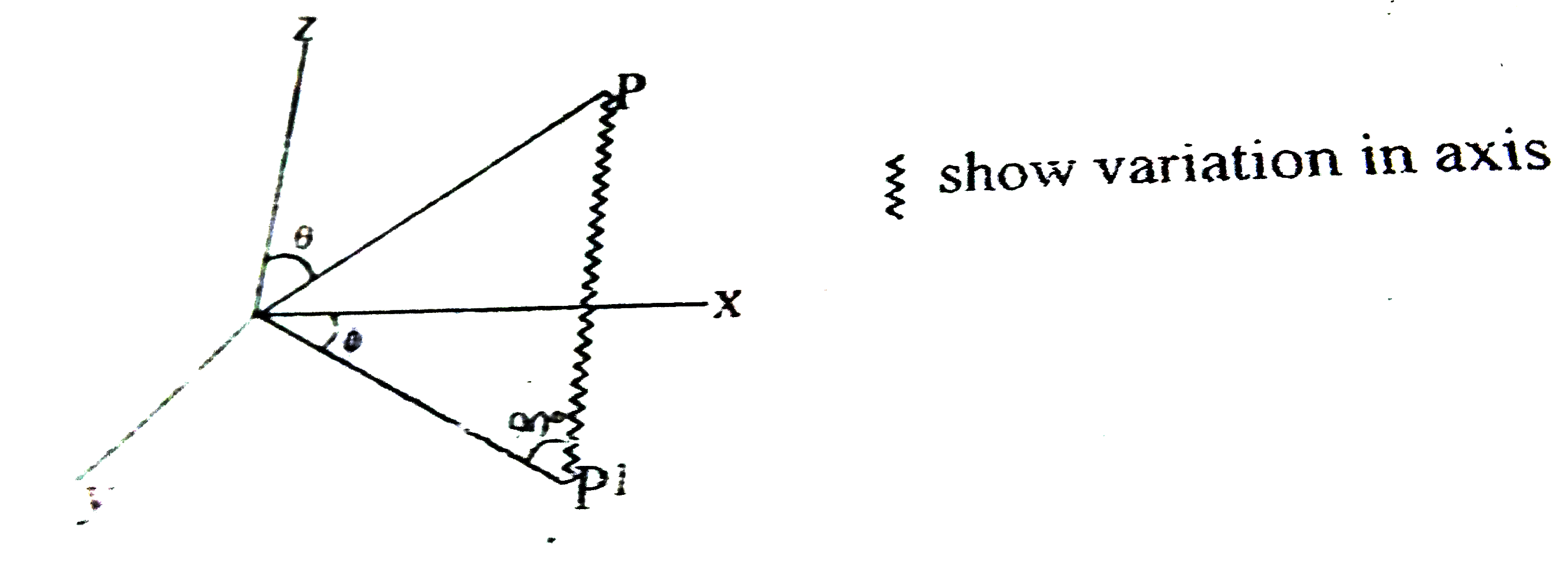
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l = 0$ are called s-electrons those occupying orbitals for which $l = 1$ are p-electrons and those for which $l = 2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n = 1, l = 0)$ we have a $1 s$ -electron, or that the electron moves in a $1 s$ -orbital. The relation of the spherical polar co-ordinates $r, θ$ and $ϕ$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $θ$ and $ϕ$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$ϕ (r, θ, ϕ) = R (r) X (θ, ϕ)$
Angular and radial parts of hydrogen atom wave function
$(Angular part X (θ, ϕ),, Radial part R_{n, l} (r)), (X (s) = {(\frac{1}{4 π})}^{1 / 2},, R (1 s) = 2 {(\frac{z}{a_{0}})}^{3 / 2} e^{- σ / 2}), (X (p_{x}) = {(\frac{3}{4 π})}^{1 / 2} sin θ cos ϕ,, R (2 s) = \frac{1}{2 \sqrt{2}} {(\frac{z}{a_{0}})}^{3 / 2} (2 - σ) e^{- σ / 2}), (X (p_{y}) = {(\frac{3}{4 π})}^{1 / 2} sin θ sin ϕ,, R (2 p) = \frac{1}{2 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} σ e^{- σ / 2}), (X (p_{z}) = {(\frac{3}{4 π})}^{1 / 2} cos θ,,), (X (d_{2}^{2}) = {(\frac{5}{16 π})}^{1 / 2} (3 {cos}^{2} θ - 1),,), (X (d_{x z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ cos ϕ,, R (3 s) = \frac{1}{9 \sqrt{3}} {(\frac{z}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}), (X (d_{y z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ sin ϕ,, R (3 p) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2}), (X (d_{x^{2} - y^{2}}^{2}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ cos 2 ϕ,, R (3 d) = \frac{1}{9 \sqrt{30}} {(\frac{z}{a_{0}})}^{3 / 2} σ^{2} e^{- σ / 2}), (X (d_{x y}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ sin 2 ϕ,,), (,, σ = \frac{2 Z r}{n a_{0}}, a_{0} = \frac{h^{2}}{4 π^{2} m e^{2}})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1 / 4 π)}^{1 / 2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., $ψ^{2}$ at that point. Thus, $ψ^{2}$ is known as probability density and always a positive quantity.
$ψ^{2} d V (or ψ^{2} . 4 π r^{2} d r)$ . represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle only
A $1 s$ and $2 s$
B $2 p_{z}$ and $2 d_{z}^{2}$
C $2 p_{x}$ and $3 d_{z}^{2}$
D $2 p_{x}$ and $2 s$
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $∣ ∣ ψ^{2} ∣ ∣$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.

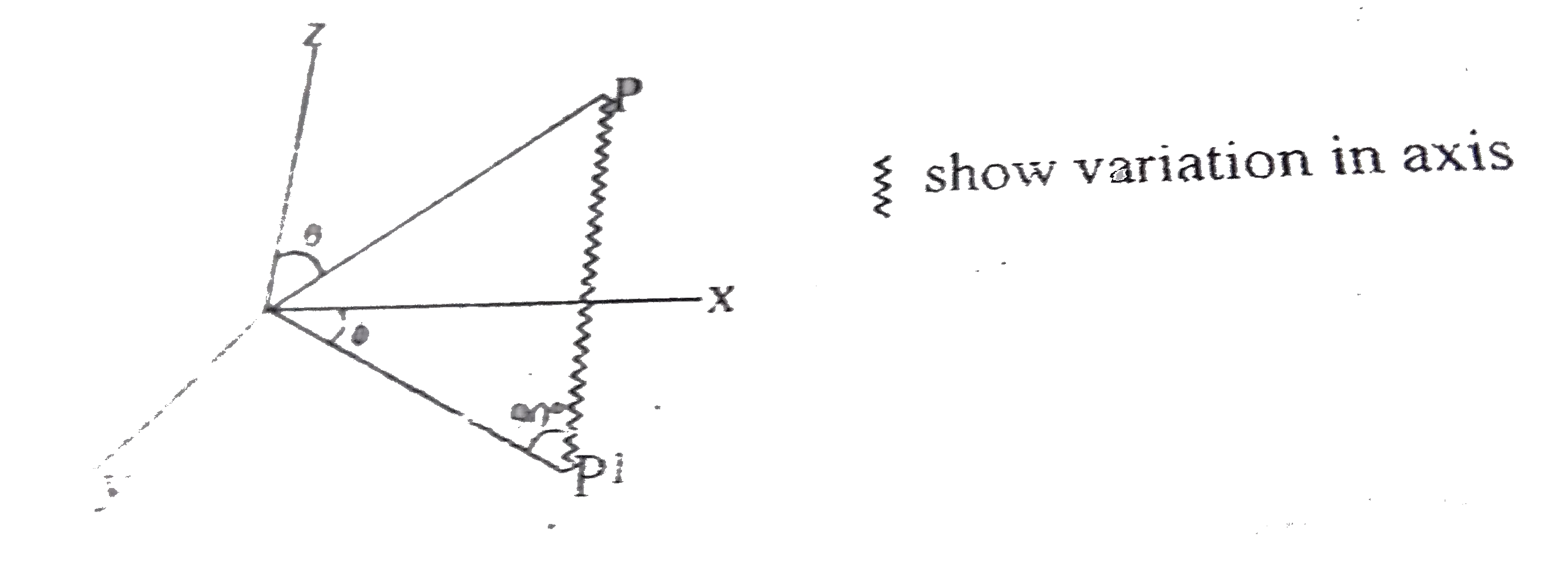
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l = 0$ are called s-electrons those occupying orbitals for which $l = 1$ are p-electrons and those for which $l = 2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n = 1, l = 0)$ we have a $1 s$ -electron, or that the electron moves in a $1 s$ -orbital. The relation of the spherical polar co-ordinates $r, θ$ and $ϕ$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $θ$ and $ϕ$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$ϕ (r, θ, ϕ) = R (r) X (θ, ϕ)$
Angular and radial parts of hydrogen atom wave function
$(Angular part X (θ, ϕ),, Radial part R_{n, l} (r)), (X (s) = {(\frac{1}{4 π})}^{1 / 2},, R (1 s) = 2 {(\frac{z}{a_{0}})}^{3 / 2} e^{- σ / 2}), (X (p_{x}) = {(\frac{3}{4 π})}^{1 / 2} sin θ cos ϕ,, R (2 s) = \frac{1}{2 \sqrt{2}} {(\frac{z}{a_{0}})}^{3 / 2} (2 - σ) e^{- σ / 2}), (X (p_{y}) = {(\frac{3}{4 π})}^{1 / 2} sin θ sin ϕ,, R (2 p) = \frac{1}{2 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} σ e^{- σ / 2}), (X (p_{z}) = {(\frac{3}{4 π})}^{1 / 2} cos θ,,), (X (d_{2}^{2}) = {(\frac{5}{16 π})}^{1 / 2} (3 {cos}^{2} θ - 1),,), (X (d_{x z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ cos ϕ,, R (3 s) = \frac{1}{9 \sqrt{3}} {(\frac{z}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}), (X (d_{y z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ sin ϕ,, R (3 p) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2}), (X (d_{x^{2} - y^{2}}^{2}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ cos 2 ϕ,, R (3 d) = \frac{1}{9 \sqrt{30}} {(\frac{z}{a_{0}})}^{3 / 2} σ^{2} e^{- σ / 2}), (X (d_{x y}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ sin 2 ϕ,,), (,, σ = \frac{2 Z r}{n a_{0}}, a_{0} = \frac{h^{2}}{4 π^{2} m e^{2}})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1 / 4 π)}^{1 / 2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., $ψ^{2}$ at that point. Thus, $ψ^{2}$ is known as probability density and always a positive quantity.
$ψ^{2} d V (or ψ^{2} . 4 π r^{2} d r)$ . represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for $1 s$ -orbital best represented by the relation.
A $\frac{1}{2 \sqrt{π}} {(\frac{Z}{a_{0}})}^{3 / 2} \times e^{\frac{r}{a_{0}}}$
B $\frac{1}{π} {(\frac{Z}{a_{0}})}^{3} \times e^{- \frac{2 z r}{a_{0}}}$
C $\frac{1}{π} {(\frac{Z}{a_{0}})}^{3 / 2} \times e^{\frac{r}{a_{0}}}$
D $\frac{2}{π} {(\frac{Z}{a_{0}})}^{3} \times e^{- \frac{2 z r}{a_{0}}}$

NCERT EXEMPLAR-LIGHT -SHORT ANSWER QUESTIONS

Home
Ask Doubt
Profile

The side mirror of a scooter got broken. The mechanic replaced it with a plane mirror. Mention any inconvenience that the driver of the scooter will face while using it?

Topper's Solved these Questions

Similar Questions

Knowledge Check

NCERT EXEMPLAR-LIGHT -SHORT ANSWER QUESTIONS