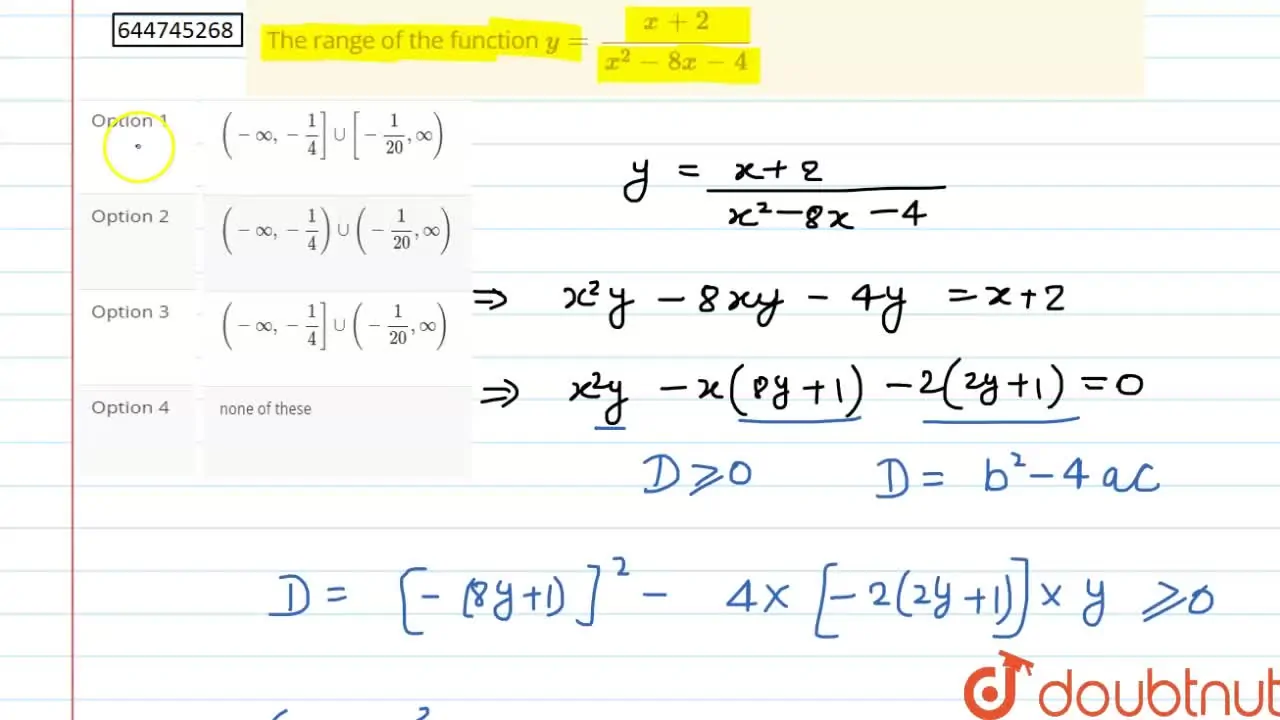
The range of the function y=x+2x2−8x−4
(−∞,−14]∪[−120,∞)
(−∞,−14)∪(−120,∞)
(−∞,−14]∪(−120,∞)
none of these
The correct Answer is:B
Step by step video & image solution for The range of the function y=(x+2)/(x^2-8x-4) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Exercise94videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test55videos
PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise63videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
Similar Questions
The range of the functiony=(x21+x2) where x ∈ R
View SolutionFind the range of the function f(x)=x2−2x−4.
View SolutionThe range of the function y=x−2/3 is
View SolutionThe range of the function f(x)=x2−2x2−3 is
View SolutionFind the range of the function y=x2−1x−1,x≠1.
View SolutionWrite the domain and range of the function f(x)=x−22−x .
View SolutionThe range of the function f(x)=x2+1x2+1 is
View SolutionThe range of the function f(x)=x2+1x2+1 is
View SolutionThe range of the function y=[x2]−[x]2 x∈[0,2] (where [] denotes the greatest integer function), is
View SolutionFind the domain and range of the function x2−4x−2
View Solution