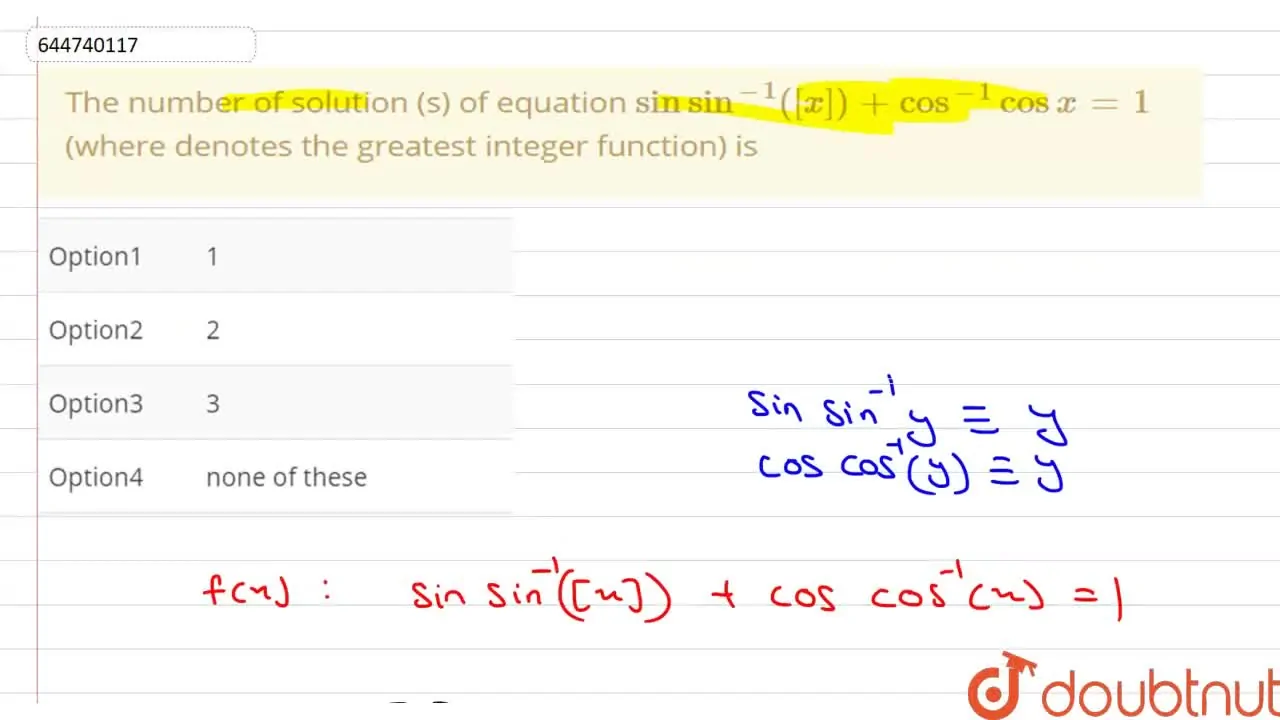
The number of solution (s) of equation sinsin−1([x])+cos−1cosx=1 (where denotes the greatest integer function) is
1
2
3
none of these
The correct Answer is:D
Step by step video & image solution for The number of solution (s) of equation sin sin^(-1)([x])+cos^(-1)cosx=1 (where denotes the greatest integer function) is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - Section II - Assertion Reason Type1videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - EXERCISE SECTION-II (Assertion-Reason )1videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - Section 2 - Assertion Reason Type9videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - HYPERBOLAEXERCISE - Chapter Test29videos
HYPERBOLA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LOGARITHMSEXERCISE - Chapter Test21videos
LOGARITHMS
Similar Questions
Sove [cot−1x]+[cos−1x]=0, where [.] denotes the greatest integer function
View Solutionf(x)=cosec−1[1+sin2x], where [⋅] denotes the greatest integer function.
View SolutionNumber of solutions of the equation cos[x]=e2x−1,x∈[0,2π], where[.] denotes the greatest integer function is
View SolutionThe number of solutions of the equation tan−1(4{x})+cot−1(x+[x]))=π2 is (where [.] denotes greatest integer function and {.} fractional part of function.
View SolutionFind number of solutions for equation [sin−1x]=x−[x], where [.] denotes the greatest integer function.
View SolutionSolution set of [sin−1x]>[cos−1x]. where [⋅] denotes greatest integer function
View Solutionlimx→0[sin−1xtan−1x]= (where [.] denotes the greatest integer function)
View SolutionRange of f(x)=sin−1[x−1]+2cos−1[x−2] ([.] denotes greatest integer function)
View SolutionIf f(x)=[sin−1(sin2x)] (where, [] denotes the greatest integer function ), then
View SolutionThe number of solution (s) of the equation sin^-1x + cos^-1(1-x)=sin^-1(-х) is/are
View Solution