The mirror image of the focus to the parabola 4(x+y)=y2 w.r.t. the directrix is
(0, 2)
(2, 2)
(-4, 2)
(-2, 2)
The correct Answer is:C
Given parabola is y2=4x+4y
⇒y2−4y=4x ⇒y2−4y+4=4x+4
⇒(y−2)2=4(x+1)
⇒Y2=4x, X=x+1
Y=y−2
∴ Focus : (a,0)
X=a=1 Y=0
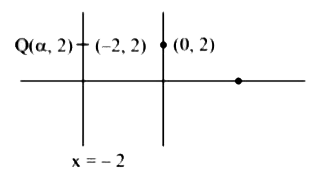
⇒ Focus : (a,0)
X=a=1 Y=0
⇒x+1=1⇒y−2=0
⇒x=0⇒y=2
F :(0,2)
Directrix : X = -a
⇒x+1=−1 ⇒x+2=0
∴α+02=−2 ⇒α=−4
Image of (0,2) = (-4,2)
Similar Questions
The focus of the parabola y2−4y−8x−4=0 is
View SolutionThe focus of the parabola y2=x+4y+3, is :
View SolutionThe focus of the parabola y2−4y−8x+4=0 is,
View SolutionFind the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.x2=6y
View SolutionFind the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.x2=−9y
View SolutionFind the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.y2=10x
View SolutionFind the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.x2=−16y
View SolutionFind the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.y2=−8x
View SolutionFind the length of the latus rectum of the parabola whose focus is at (2, 3) and directrix is the line x−4y+3=0 .
View SolutionFind the length of the latus rectum of the parabola whose focus is at (2, 3) and directrix is the line x−4y+3=0 .
View Solution
