vertex and focus of a parabola are (-1,1) and (2,3) respectively. find the equation of the directrix.
3x+2y+14=0
3x+2y−25=0
2x−3y+10=0
x−y+5=0
The correct Answer is:A
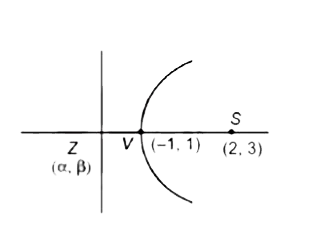
As we know that, vertex is the mid-point of the perpendicular drop from the focus of the directrix.
α+22=−1⇒α+2=−2⇒α=−4
β+32=1⇒β=2−3=−1
Slope of axis of the parabola =3−β2−α=3+12+4=23
Slope of the directrix =−32
Equation of directrix is
y+1=−32(x+4)
2y+2=−3x−12
3x+2y+14=0
Similar Questions
If the vertex and focus of a parabola are (3,3) and (−3,3) respectively, then its equation is
View SolutionIf the focus and the vertex of a parabola are (2,3) and (-1,1) respectively, then the directrix is :
View SolutionIf the focus and vertex of a parabola are the points (0, 2) and (0, 4), respectively, then find the equation
View SolutionIf the focus and vertex of a parabola are the points (0, 2) and (0, 4), respectively, then find the equation
View SolutionIf the focus of a parabola is (-2,1) and the directrix has the equation x+y=3 then its vertex is a. (0,3) b. (-1,1/2) c. (-1,2) d. (2,-1)
View SolutionIf the points (0,4)and(0,2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
View SolutionIf the points (0,4)and(0,2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
View SolutionFind the equation of the parabola with focus (−3,0) and the equation of the directrix is x = 3.
View SolutionThe focus and directrix of a parabola are (1, 2) and x + 2y + 9 = 0 then equation of tangent at vertex is
View SolutionFind the equation of the parabola whose focus is (−1,−2) and the equation of the directrix is given by 4x−3y+2=0. Also find the equation of the axis.
View Solution
