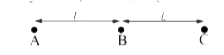
Three particles A, B and C of mass m, m and 2m lie in a straight line as shown. The only force acting on these particles is due to the gravitational attraction towards each other. Let the magnitude of net force on them be FA,FB and FC respectively. Then,FA:FB:FC is equal to :
3:2:5
3:1:4
2:2:3
6:1:5
The correct Answer is:A
Taking rightward direction as positive,
FA=G(m)(m)L2ˆi+G(m)(2m)(2L)2ˆi=32Gm2L2ˆi
FB=−G(m)(m)L2ˆi+G(m)(2m)L2ˆi=Gm2L2
FC=−G(2m)(m)(2L)2ˆi−G(2m)(m)L2ˆi=−52Gm2L2ˆi
So, |FA|:|FB|:|FC|=32:1:52=3:2:5
Topper's Solved these Questions
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- JEE MAIN REVISION TEST - 30 | JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 30 | JEE -2020EXERCISE - PHYSICS
25 Videos
Similar Questions
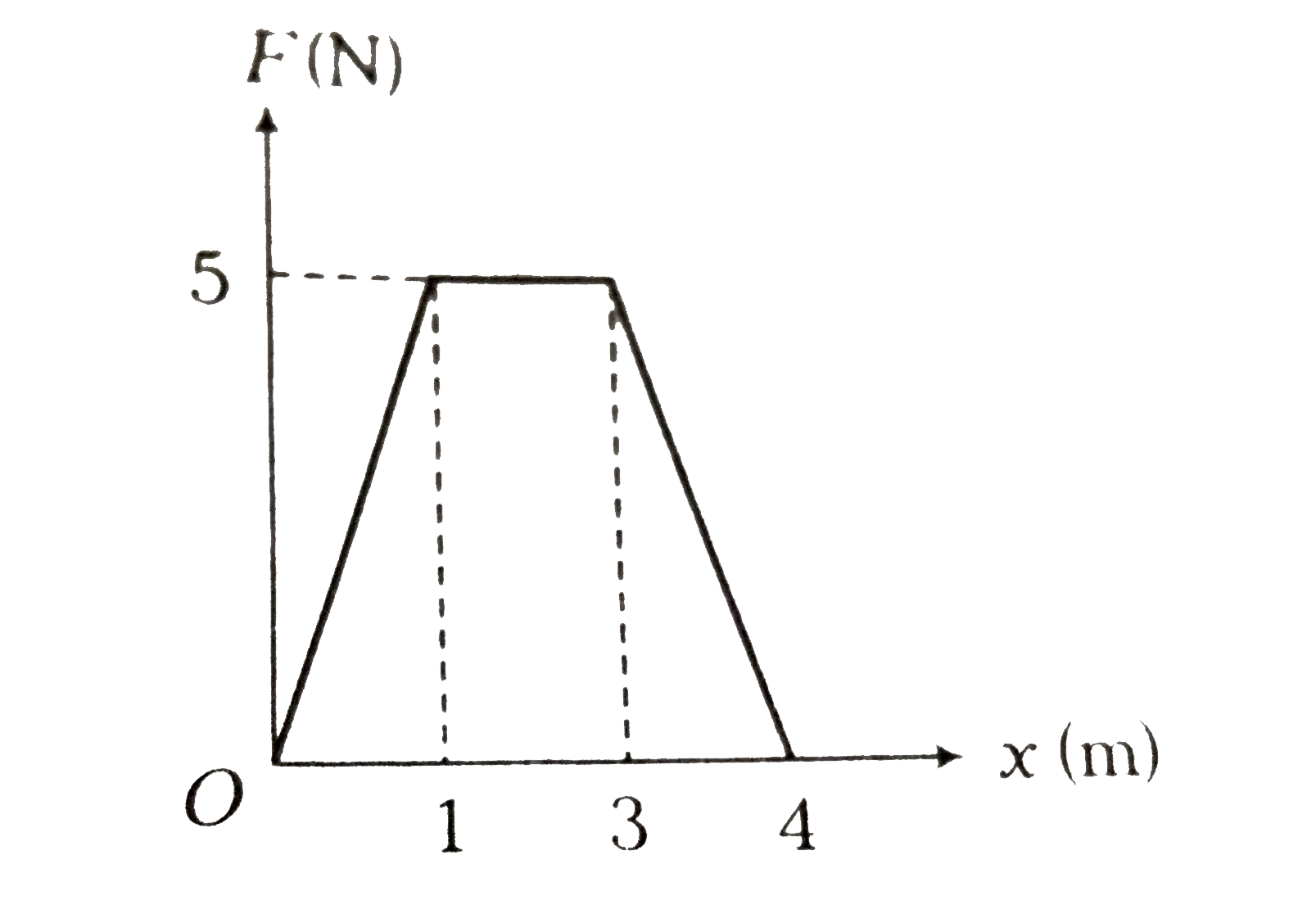
The force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
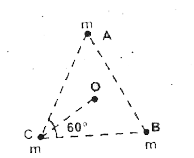
Force acting on particle C, due to particle A and B
View Solution
Knowledge Check
A block of mass m slides with constant speed down a ramp whose incline angle is θ. If F1 is the magnitude of the gravitational force acting parallel to the ramp and F2 is the magnitude of the normal force acting on the block, what is the value of F1/F2?
Am tan θBm cot θC1Dtan θ
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionLet F1 be the magnitude of the gravitational force exerted on the Sun by Earth and F2 be the magnitude of the force exerted on Earth by the Sun. Then:
View SolutionStatement I: Two particle are moving towards each other due to mutual gravitational attraction. The momentum of each particle will increase.
Statement II: The rate of change of momentum depends upon Fext.
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
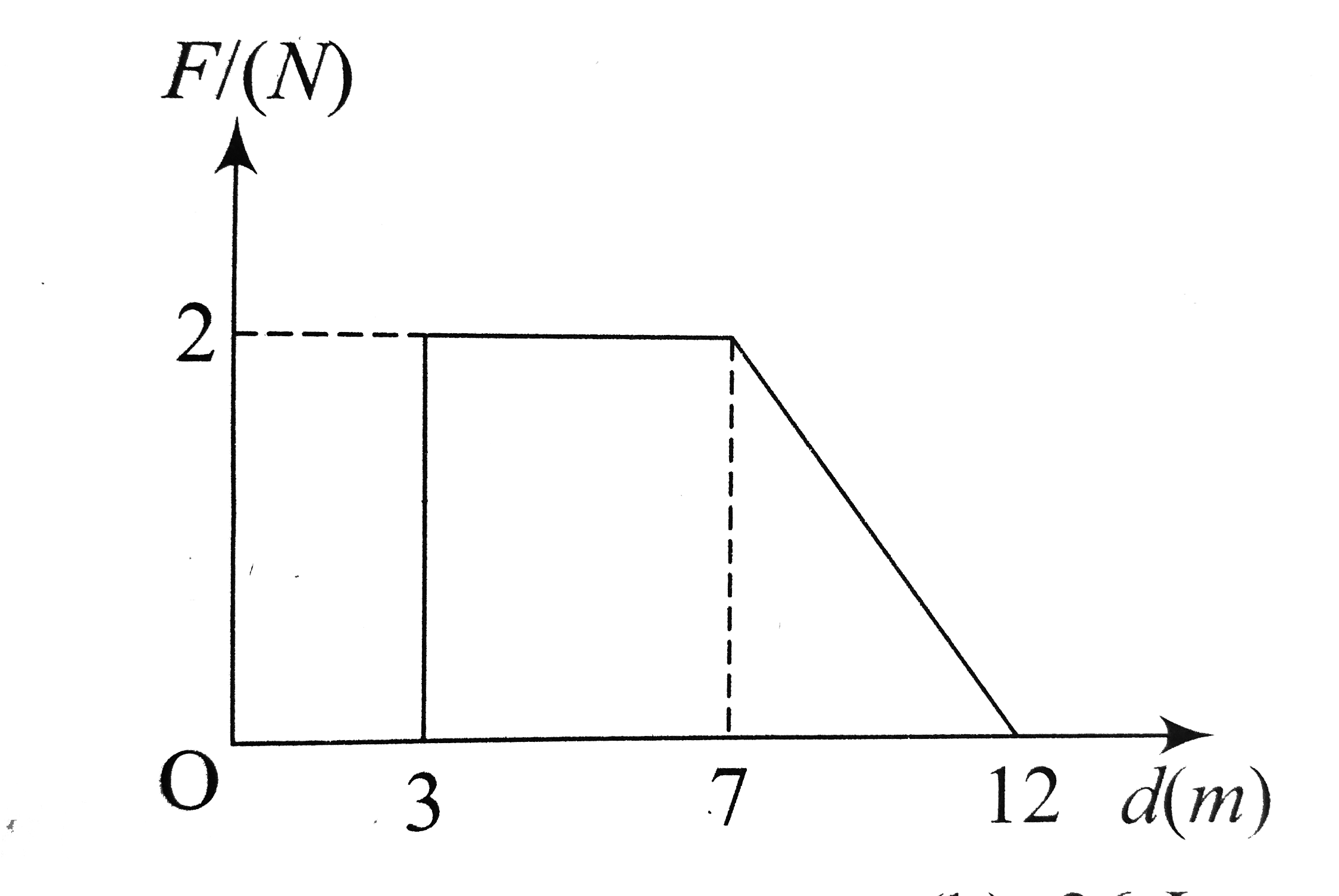
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
View SolutionTwo forces of mangitude F1 and F2 are acting on an object.The magnitude of the net force Fnet on the object will be in the range.
View Solution
