The locus of a point which divides a line segment AB=4 cm in 1 : 2, where A lies on the line y=x and B lies on the y=2x is

A

$234 x^{2} + 153 y^{2} - 378 x y - 32 = 0$

B

$234 x^{2} + 153 y^{2} - 378 x y + 32 = 0$

C

$234 x^{2} + 153 y^{2} + 378 x y + 32 = 0$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

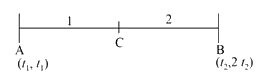
$3 h = t_{2} + 2 t_{1}$
$3 k = 2 t_{2} + 2 t_{1}$
$t_{2} = 3 k - 3 h$
$3 h = 3 k - 3 h + 2 t_{1}$
$\frac{6 h - 3 k}{2} = t_{1}$
${(t_{1} - t_{2})}_{1}^{2} + {(t_{1} + 2 t_{2})}_{1}^{2} = 16$
${(\frac{6 h - 3 k}{2} - 3 k + 3 h)}^{2} + {(\frac{6 h - 3 k}{2} - 6 k + 6 h)}^{2} = 16$
$\frac{{(6 h - 3 k - 6 k + 6 h)}^{2}}{4} + \frac{{(6 h - 3 k - 12 k + 12 h)}^{2}}{4} = 64$
${(12 h - 9 k)}^{2} + {(18 h - 15 k)}^{2} = 64$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The ratio in which the line segment joining (-1,1) and (5,7) is divided by the line $x + y = 4$ is
A $1 : 2$ internally
B $1 : 2$ externally
C $2 : 1$ internally
D $2 : 1$ externally

VMC MODULES ENGLISH-MOCK TEST 5-MATHEMATICS (SECTION 2)

Home
Ask Doubt
Profile