If a circle of radius $3$ units is touching the lines $\sqrt{3} y^{2} - 4 x y + \sqrt{3} x^{2} = 0$ in the first quadrant then the length of chord of contact to this circle, is:

A

$\frac{\sqrt{3} + 1}{2}$

B

$\frac{\sqrt{3} + 1}{\sqrt{2}}$

C

$3 (\frac{\sqrt{3} + 1}{\sqrt{2}})$

D

$\frac{3 (\sqrt{3} + 1)}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

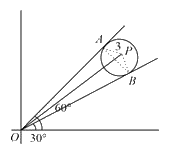
Given equation of lines $\sqrt{3} y^{2} - 4 x y + \sqrt{3} x^{2} = 0$
$\sqrt{3} y^{2} - 3 x y - x y + \sqrt{3} x^{2} = 0$
$\Rightarrow (\sqrt{3} y - x) (y - \sqrt{3} x) = 0 \Rightarrow y = \frac{x}{\sqrt{3}}, y = \sqrt{3} x$
$∠ A P O = 75^{\circ}$
Length of chord of contact AB
$= 2.3 {sin 75}^{\circ} = 6 ({sin 45}^{\circ} {cos 30}^{\circ} + {sin 30}^{\circ} {cos 45}^{\circ})$
$6 (\frac{1}{\sqrt{2}} . \frac{\sqrt{3}}{2} + \frac{1}{2} . \frac{1}{\sqrt{2}}) = \frac{6 (\sqrt{3} + 1)}{2 \sqrt{2}} = \frac{3 (\sqrt{3} + 1)}{\sqrt{2}}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-MOCK TEST 5-MATHEMATICS (SECTION 2)

Home
Ask Doubt
Profile