Consider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is ϕ0 then the magnetic flux through the other circular base will be:
ϕ0
>ϕ0
−ϕ0
<ϕ0
The correct Answer is:C
To solve the problem, we need to analyze the magnetic flux through the two circular bases of a cylindrical surface that encloses a short bar magnet placed at the center.
1. Understanding the Setup:
- We have a cylindrical surface with a bar magnet placed at its center.
- The bar magnet has a North Pole and a South Pole.
Hint: Visualize the setup by sketching a cylinder with a bar magnet in the middle. Identify the North and South poles.
2. Magnetic Flux Definition:
- Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) through which it passes, considering the angle (θ) between the field lines and the normal to the surface:
Φ=B⋅A⋅cos(θ)
Hint: Remember that the angle θ is important when calculating flux; it affects how much of the magnetic field passes through the surface.
3. Magnetic Field Lines:
- The magnetic field lines emerge from the North Pole and terminate at the South Pole. Since the magnet is symmetrically placed in the cylinder, the field lines will be evenly distributed.
Hint: Think about how the magnetic field lines behave in a dipole configuration. They spread out from the North and converge at the South.
4. Flux through the Circular Bases:
- Let’s denote the flux through the top circular base as Φ₁ and the flux through the bottom circular base as Φ₂.
- Given that the flux through one of the bases is Φ₀, we can say:
Φ1=Φ0
- Since the magnet is symmetrically placed, the flux entering through the North Pole will equal the flux exiting through the South Pole.
Hint: Consider the conservation of magnetic field lines. The number of lines entering one base must equal the number exiting the other.
5. Applying Gauss's Law for Magnetism:
- According to Gauss's law for magnetism, the total magnetic flux through a closed surface is zero:
Φtotal=Φ1+Φ2+Φcurved surface=0
- Since the curved surface does not contribute to the net flux (it is enclosed), we have:
Φ1+Φ2=0
Hint: Remember that the net flux through a closed surface surrounding a magnet is zero.
6. Finding the Flux through the Other Base:
- From the equation above, if Φ₁ = Φ₀, then:
Φ0+Φ2=0⟹Φ2=−Φ0
- Therefore, the flux through the other circular base is:
Φ2=−Φ0
Hint: The negative sign indicates that the direction of the magnetic field through the second base is opposite to that through the first base.
Final Answer:
The magnetic flux through the other circular base will be:
Φ2=−Φ0
- We have a cylindrical surface with a bar magnet placed at its center.
- The bar magnet has a North Pole and a South Pole.
- Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) through which it passes, considering the angle (θ) between the field lines and the normal to the surface:
Φ=B⋅A⋅cos(θ)
- The magnetic field lines emerge from the North Pole and terminate at the South Pole. Since the magnet is symmetrically placed in the cylinder, the field lines will be evenly distributed.
- Let’s denote the flux through the top circular base as Φ₁ and the flux through the bottom circular base as Φ₂.
- Given that the flux through one of the bases is Φ₀, we can say:
Φ1=Φ0
- Since the magnet is symmetrically placed, the flux entering through the North Pole will equal the flux exiting through the South Pole.
- According to Gauss's law for magnetism, the total magnetic flux through a closed surface is zero:
Φtotal=Φ1+Φ2+Φcurved surface=0
- Since the curved surface does not contribute to the net flux (it is enclosed), we have:
Φ1+Φ2=0
- From the equation above, if Φ₁ = Φ₀, then:
Φ0+Φ2=0⟹Φ2=−Φ0
- Therefore, the flux through the other circular base is:
Φ2=−Φ0
The magnetic flux through the other circular base will be:
Φ2=−Φ0
Topper's Solved these Questions
Similar Questions
If the magnetic field is parallel to a surface then, the magnetic flux through the surface is
View SolutionA current carrying circular loop is placed in an infinite plane if ϕi is the magnetic flux through the inner region and ϕo is magnitude of magnetic flux through the outer region, then
View Solution
Knowledge Check
The net magnetic flux through any closed surface, kept in a magnetic field is
AzeroBμ04πC4πμ0D4μ0π
A current carrying circular loop is placed in an infinite plane if ϕi is the magnetic flux through the inner region and ϕo is magnitude of magnetic flux through the outer region, then
View SolutionA circular coil, carrying a constant current i s kept in the x - y plane. The magnetic flux through the entire x - y plane exluding the area of the circular coil is given by ϕ and the magetic flux through the area of the circular coil area is given by ϕ0, then
View SolutionConsider a rectangular coil of wire carrying constant current I, forming a magnetic dipole. The magnetic flux through an infinite plane that contains the circular coil and excluding the rectangular area is given by ϕi. The magnetic flux through the area of the rectangular area is given by ϕ0. Which of the following option is correct?
View SolutionThe net magnetic flux through any closed surface, kept in a magnetic field is
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
View Solution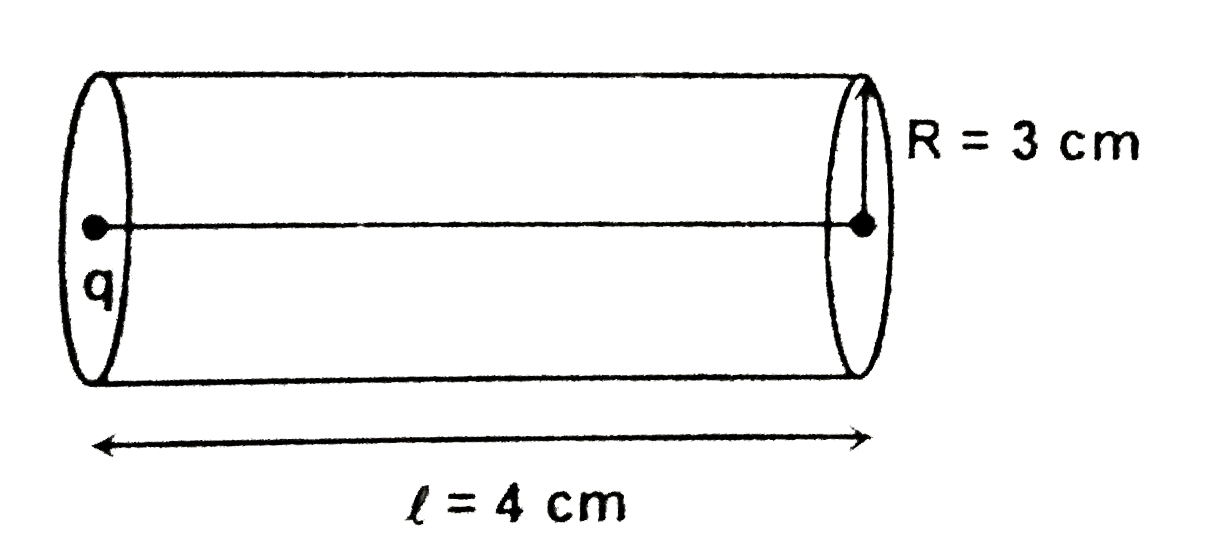
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder is
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
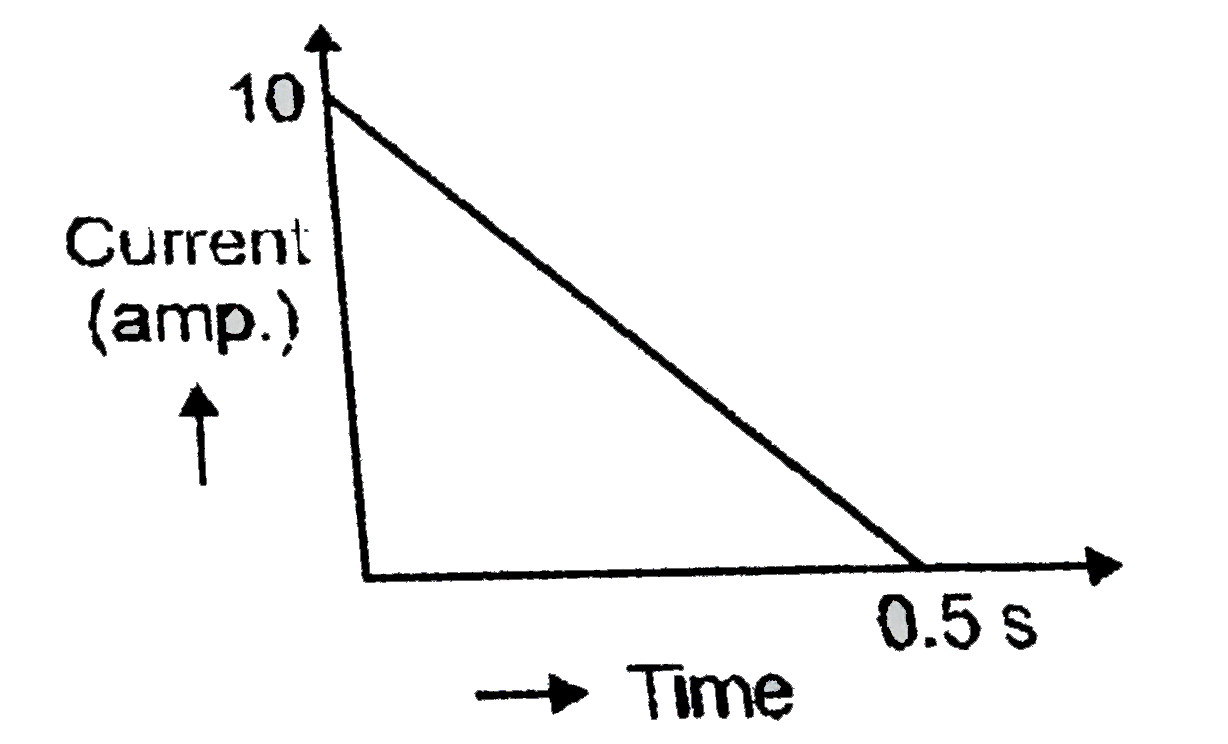
View Solution
