When a light ray is incident on a medium of refractive index 4/3, reflected light is found to be 100% polarized. What is the angle of refraction in degrees?
(tan53∘=43).
The correct Answer is:37
To solve the problem, we can follow these steps:
Step 1: Understand the concept of Brewster's Angle
When light is incident on a medium and the reflected light is 100% polarized, it occurs at Brewster's angle (θ_B). At this angle, the reflected and refracted rays are perpendicular to each other.
Step 2: Set up the relationship between angles
At Brewster's angle, we have:
I+R=90∘
where I is the angle of incidence and R is the angle of refraction. Therefore, we can express the angle of incidence as:
I=90∘−R
Step 3: Use Snell's Law
According to Snell's Law:
μ1sinI=μ2sinR
where μ1 is the refractive index of air (approximately 1) and μ2 is the refractive index of the medium (given as 4/3). Thus, we can write:
1⋅sinI=43sinR
Step 4: Substitute for I
Substituting I=90∘−R into Snell's Law gives:
sin(90∘−R)=43sinR
Using the identity sin(90∘−R)=cosR, we have:
cosR=43sinR
Step 5: Rearranging the equation
Rearranging the equation gives:
cosRsinR=43
This can be rewritten as:
cotR=43
Step 6: Finding the angle R
To find R, we can take the cotangent inverse:
R=cot−1(43)
Using the known value, we find:
R≈37∘
Final Answer
The angle of refraction R is approximately 37∘.
---
When light is incident on a medium and the reflected light is 100% polarized, it occurs at Brewster's angle (θ_B). At this angle, the reflected and refracted rays are perpendicular to each other.
At Brewster's angle, we have:
I+R=90∘
where I is the angle of incidence and R is the angle of refraction. Therefore, we can express the angle of incidence as:
I=90∘−R
According to Snell's Law:
μ1sinI=μ2sinR
where μ1 is the refractive index of air (approximately 1) and μ2 is the refractive index of the medium (given as 4/3). Thus, we can write:
1⋅sinI=43sinR
Substituting I=90∘−R into Snell's Law gives:
sin(90∘−R)=43sinR
Using the identity sin(90∘−R)=cosR, we have:
cosR=43sinR
Rearranging the equation gives:
cosRsinR=43
This can be rewritten as:
cotR=43
To find R, we can take the cotangent inverse:
R=cot−1(43)
Using the known value, we find:
R≈37∘
The angle of refraction R is approximately 37∘.
Topper's Solved these Questions
- MOCK TEST 2BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 2EXERCISE - PART I : PHYSICS (SECTION - 2)
10 Videos
- MOCK TEST 13BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 13EXERCISE - PHYSICS ( SECTION -2)
5 Videos
- MOCK TEST 3BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 3EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
A ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionWhen light of a certain wavelength is incident on a plane surface of a material at a glancing angle 30∘, the reflected light is found to be completely plane polarized Determine
Angle of refraction.
View SolutionA light ray incidents on water (n=43) surface from air and reflected from air and reflected part of it is found to be polarized. Find the deviation of refracted light from its original path:
View SolutionUnpolarized light is incident on a plane surface of glass of refractive index μ at angle i. If the reflected light gets totally polarized, write the relation between the angle i and refractive index μ.
View SolutionA beam of light travelling in water strikes a glass plate, which is also immersed in water. When the angle of incidence is 51∘, the reflected beam is found to be plane polarised . What is the refractive index of glass if the refractive index of water is 43? [tan51∘=1.235]
View SolutionThe angle of incidence of a light beam onto a reflecting surface is continuously varied. The reflected ray is found to be completely polarized when the angle of incidence is 60∘. What is the index of refraction of the reflecting material ?
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?

View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
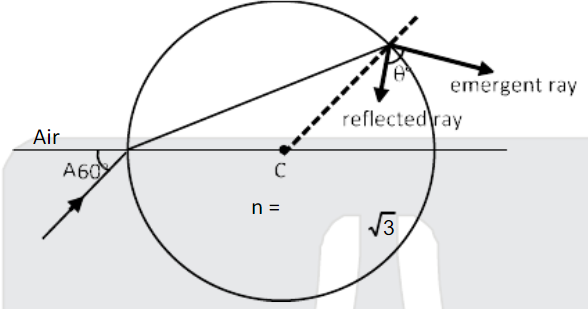
View SolutionWhen the angle of incidence on a material is 60∘, the reflected light is completely polarized. The velocity of the refracted ray inside the material is (in ms−1)
View SolutionWhen the angle of incidence on a material is 60∘, the reflected light is completely polarized. The velocity of the refracted ray inside the material is (in ms−1)
View Solution
