A vertical pole of length 15 m standing on the point A. ABC are points on horizontal ground forming a triangle with ∠A=90∘.
If AB = 6m and AC = 8m and a point 'D' (on horizontal plane) is equidistant from A, B, C. Find distance of D from top of the pole
5√10m
10√5m
6√10m
None of these
The correct Answer is:A
To solve the problem, we need to find the distance from point D (which is equidistant from points A, B, and C) to the top of the vertical pole at point A. Let's break down the solution step by step.
Step 1: Understand the triangle ABC
We have a right triangle ABC with:
- Angle A = 90°
- AB = 6 m
- AC = 8 m
Using the Pythagorean theorem, we can find the length of the hypotenuse BC.
Step 2: Calculate the length of BC
Using the Pythagorean theorem:
BC=√AB2+AC2=√62+82=√36+64=√100=10 m
Step 3: Find the coordinates of points A, B, and C
Assuming point A is at the origin (0, 0):
- Point B can be at (6, 0) since AB = 6 m along the x-axis.
- Point C can be at (0, 8) since AC = 8 m along the y-axis.
Thus, the coordinates are:
- A(0, 0)
- B(6, 0)
- C(0, 8)
Step 4: Find the midpoint D of hypotenuse BC
The coordinates of point D, which is the midpoint of BC, can be calculated as:
D(xB+xC2,yB+yC2)=D(6+02,0+82)=D(3,4)
Step 5: Determine the height of the pole
The height of the vertical pole at point A is given as 15 m. Therefore, the coordinates of the top of the pole (point P) are:
- P(0, 0, 15)
Step 6: Calculate the distance PD from point D to the top of the pole P
To find the distance PD, we use the 3D distance formula:
PD=√(xP−xD)2+(yP−yD)2+(zP−zD)2
Substituting the coordinates:
PD=√(0−3)2+(0−4)2+(15−0)2
PD=√(−3)2+(−4)2+(15)2
PD=√9+16+225=√250
PD=√25×10=5√10 m
Final Answer
The distance from point D to the top of the pole is 5√10 meters.
---
We have a right triangle ABC with:
- Angle A = 90°
- AB = 6 m
- AC = 8 m
Using the Pythagorean theorem:
BC=√AB2+AC2=√62+82=√36+64=√100=10 m
Assuming point A is at the origin (0, 0):
- Point B can be at (6, 0) since AB = 6 m along the x-axis.
- Point C can be at (0, 8) since AC = 8 m along the y-axis.
- A(0, 0)
- B(6, 0)
- C(0, 8)
The coordinates of point D, which is the midpoint of BC, can be calculated as:
D(xB+xC2,yB+yC2)=D(6+02,0+82)=D(3,4)
The height of the vertical pole at point A is given as 15 m. Therefore, the coordinates of the top of the pole (point P) are:
- P(0, 0, 15)
To find the distance PD, we use the 3D distance formula:
PD=√(xP−xD)2+(yP−yD)2+(zP−zD)2
Substituting the coordinates:
PD=√(0−3)2+(0−4)2+(15−0)2
PD=√(−3)2+(−4)2+(15)2
PD=√9+16+225=√250
PD=√25×10=5√10 m
The distance from point D to the top of the pole is 5√10 meters.
Topper's Solved these Questions
- MOCK TEST 3Book:VMC MODULES ENGLISHChapter:MOCK TEST 3Exercise:PART III : MATHEMATICS (SECTION-2)
Explore 10 Videos
- MOCK TEST 2Book:VMC MODULES ENGLISHChapter:MOCK TEST 2Exercise:PART III : MATHEMATICS (SECTION - 2)
Explore 10 Videos
- MOCK TEST 4Book:VMC MODULES ENGLISHChapter:MOCK TEST 4Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
Similar Questions
Construct a triangle ABC in which AB = 6cm, BC= 7 cm and CA = 6.5 cm. Find a point P equidistant from B and C, and also equidistant from AB and BC.
View SolutionConstruct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC=105∘. Hence
Construct the locus of points equidistant from BA and BC.
View SolutionConstruct a triangle ABC, with AB =6 cm, AC = BC = 9 cm.Find a point 4cm from A and equidistant from B and C.
View SolutionIn a triangle ABC, AB = 5 , BC = 7, AC = 6. A point P is in the plane such that it is at distance '2' units from AB and 3 units form AC then its distance from BC
View SolutionConstruct a triangle ABC, having given AB = 4.8 cm, AC = 4 cm and ∠A=75∘, Find a point P
(i) inside the triangle ABC,
(ii) outside the triangle ABC
equidistant from B and C, and at a distance of 1.2 cm from BC.
View SolutionTwo vertical poles AL and BM of height 4 m and 16 m respectively stand apart on a horizontal plane. If A, B be the feet of the poles and AM and BL intersect at P, then the height of P from the horizontal plane is equal to
View SolutionThe upper 34 th portion of a vertical pole subtends an angle θ such that tan θ=35 at a point in the horizontal plane through its foot and at a distance 40m from the foot. Find the possible height of the vertical pole.
View SolutionABC is a triangle. Locate a point in the interior of ΔABCwhich is equidistant from all the vertices of ΔABC
View SolutionConstruct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC, and also 2 cm from BC. Measure the distance between the two points obtained.
View SolutionIn figure , the angle of elevation of the top of a tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m, Find the distance of the point from the foot of the power .
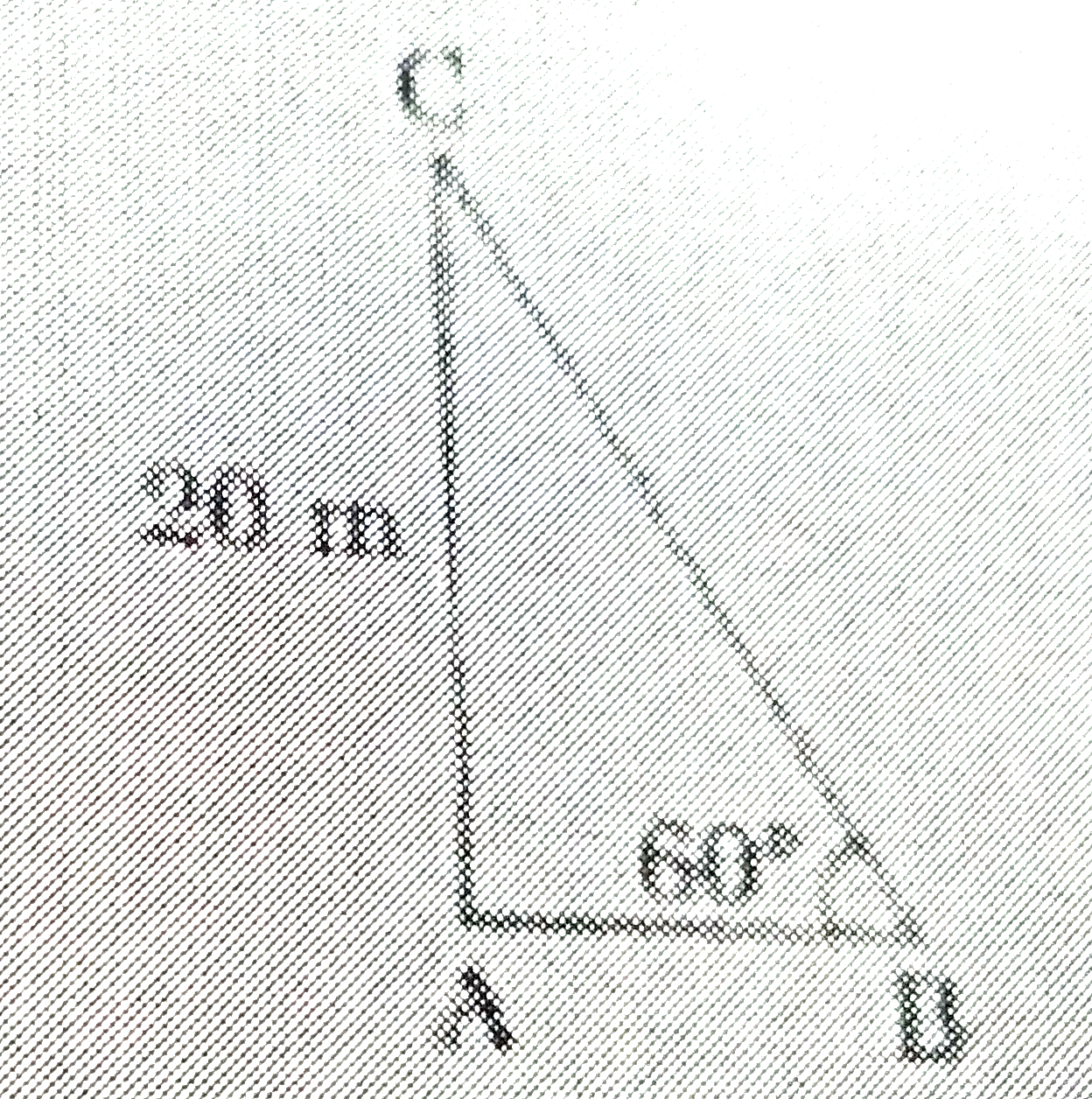
View Solution