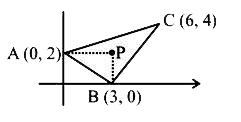
Let A(0,2),B(3,0),C(6,4) be the vertices of triangle and P is a point inside the triangle such that area of triangle APB, BPC and CPA are equal. Equation of circle circumscribing ΔAPB is :
x2+y2−2x−3y=0
x2+y2−4x−3y=0
x2+y2−3x−4y=0
x2+y2−3x2y=0
The correct Answer is:D
ΔPAB=ΔPBC=ΔPCA ⇒ P is centroid
P(3,2)
Also ΔAPB is a night angle .
Circumcirle ⇒(x−0)(x−3)+(y−2)(y−0)=0
⇒ x2+y2−3x−2y=0
Topper's Solved these Questions
- MOCK TEST 10Book:VMC MODULES ENGLISHChapter:MOCK TEST 10Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART III : MATHEMATICS (SECTION-2)
Explore 10 Videos
- MOCK TEST 11Book:VMC MODULES ENGLISHChapter:MOCK TEST 11Exercise:MATHEMATICS (Section-2)
Explore 5 Videos
Similar Questions
Let A(5,−3),B(2,7)andC(−1,2) be the vertices of a △ABC. If P is a point inside the triangle ABC such that the triangle APC,APB and BPC have equal areas, then length of the line segment PB is:
View SolutionLet A(1,0),B(6,2) and C(32,6) be the vertices of a triangle ABC. If P is a point inside the triangle ABC such that the triangles APC, APB and BPC have equal areas , then the length of the line segment PQ, where Q is the point (−76,−13), is _________.
View Solution(6,0),(0,6)and(7,7) are the vertices of a triangle. The circle inscribed in the triangle has the equation
View SolutionA (1, -5), B (2, 2) and C (-2, 4) are the vertices of triangle ABC. find the equation of:
the median of the triangle through A.
View SolutionLet A≡(6,7),B≡(2,3)andC≡(−2,1) be the vertices of a triangle. Find the point P in the interior of the triangle such that PBC is an equilateral triangle.
View SolutionThe points A(3,1) , B (12,-2) and C(0,2) cannot be vertices of a triangle.
View SolutionA (4,2), B(6,8) and C (8,4) are the vertices of a triangle ABC. Write down the equation of the median of the triangle through A.
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are a. (43,3) b. (3,23) c. (3,43) d. (43,23)
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are (43,3) (b) (3,23) (3,43) (d) (43,23)
View SolutionProve that the points A (1,-3) B (-3,0) and C(4,1) are the vertices of an isosceles right angle triangle. Find the area of the triangle.
View Solution