Let α,β be the roots of equation x2−x+1=0 and the matrix A=1√3∣∣ ∣ ∣∣1111αα21β−β2∣∣ ∣ ∣∣ , the value of det (A.AT) is
13
1
−1
3
The correct Answer is:C
∵ 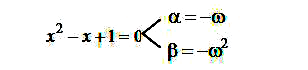
A=1√3⎡⎢⎣1111−ω−ω21−ω2−ω4⎤⎥⎦,det(A.AT)=|A|2
=13∣∣
∣
∣∣1−1−11ωω21ω2ω∣∣
∣
∣∣,∵ω3=1,1+ω+ω2=0
=13(ω2−ω4+ω−ω2+ω−ω2)2
=13(ω−ω2)2=13(ω2+ω4−2ω3)
=13(−1−2)=−1
det (A.AT)=-1
Topper's Solved these Questions
- MOCK TEST 10BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 10EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART III : MATHEMATICS (SECTION-2)
10 Videos
- MOCK TEST 11BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 11EXERCISE - MATHEMATICS (Section-2)
5 Videos
Similar Questions
Let α,andβ are the roots of the equation x2+x+1=0 then
View SolutionLet α be a root of the equation x2+x+1=0 and the matrix A=1√3⎡⎢⎣1111αα21α2α4⎤⎥⎦
then the matrix A31 is equal to :
View SolutionLet α,β are the roots of the equation x2+x+1=0, then α3−β3
View SolutionIf α,β are roots of the equation x2+x+1=0, then the equation whose roots are αβandβα, is
View SolutionIf α,β are the roots of the equation x2+x+1=0, find the value of α3−β3.
View Solutionαandβ are the roots of the equation x2−3x+5=0, the equation whose roots are 1αand1β is:
View SolutionIf α,β are the roots of x2−√3x+1=0 then α21+β21 is:
View SolutionLet α and β be the roots of the equation x2+x+1=0.
Then, for y≠0 in R.
⎡⎢⎣y+1αβαy+β1β1y+α⎤⎥⎦ is
View SolutionLet αandβ, be the roots of the equation x2+x+1=0. The equation whose roots are α19 and β7 are:
View SolutionIf α,β are the roots of 2x2+5x+2=0, then the equation with roots 1α+1,1β+1 is
View Solution
