A particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
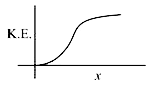
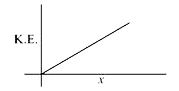
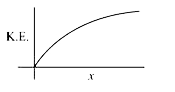
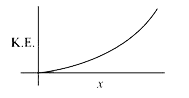
The correct Answer is:B
To solve the problem of how the kinetic energy of a charged particle changes as it travels through a uniform electric field, we can follow these steps:
Step 1: Understand the problem
We have a particle of mass m and charge q that is released from rest in a uniform electric field E. We need to find the relationship between its kinetic energy K and the distance x it travels.
Hint: Remember that the particle starts from rest, which means its initial velocity is zero.
Step 2: Determine the force acting on the particle
The only force acting on the particle due to the electric field is given by:
F=qE
Hint: The force on a charged particle in an electric field is the product of the charge and the electric field strength.
Step 3: Calculate the acceleration of the particle
Using Newton's second law, we can find the acceleration a of the particle:
a=Fm=qEm
Hint: Acceleration is the force divided by mass.
Step 4: Use kinematics to find the final velocity
Since the particle starts from rest, we can use the kinematic equation:
v2=u2+2as
Here, u=0 (initial velocity), a=qEm, and s=x (distance traveled). Thus, we have:
v2=0+2(qEm)x
This simplifies to:
v2=2qExm
Hint: This equation relates the final velocity to the distance traveled.
Step 5: Find the kinetic energy
The kinetic energy K of the particle is given by:
K=12mv2
Substituting the expression for v2:
K=12m(2qExm)
This simplifies to:
K=qEx
Hint: The kinetic energy is directly related to the distance traveled in the electric field.
Step 6: Analyze the relationship
From the equation K=qEx, we see that the kinetic energy K is directly proportional to the distance x. This indicates a linear relationship.
Hint: A linear relationship means that if you plot K against x, you will get a straight line that passes through the origin.
Step 7: Choose the correct graph
Given the options (A, B, C, D), the graph that represents a straight line passing through the origin is the correct answer.
Final Answer: The correct graph is option B.
We have a particle of mass m and charge q that is released from rest in a uniform electric field E. We need to find the relationship between its kinetic energy K and the distance x it travels.
The only force acting on the particle due to the electric field is given by:
F=qE
Using Newton's second law, we can find the acceleration a of the particle:
a=Fm=qEm
Since the particle starts from rest, we can use the kinematic equation:
v2=u2+2as
Here, u=0 (initial velocity), a=qEm, and s=x (distance traveled). Thus, we have:
v2=0+2(qEm)x
This simplifies to:
v2=2qExm
The kinetic energy K of the particle is given by:
K=12mv2
Substituting the expression for v2:
K=12m(2qExm)
This simplifies to:
K=qEx
From the equation K=qEx, we see that the kinetic energy K is directly proportional to the distance x. This indicates a linear relationship.
Given the options (A, B, C, D), the graph that represents a straight line passing through the origin is the correct answer.
Topper's Solved these Questions
Similar Questions
A particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View SolutionA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View Solution
Knowledge Check
A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
Aremains a constant because the electric field is uniform.Bincreases because the charge moves along the electric field.Cdecreases because the charge moves along the electric field.Ddecreases because the charge moves opposite to the electric field.
A particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance y between the plates.
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View Solution

