A coil of wire having inductance and resistance has a conducting ring placed coaxially within it. The coil is connected to a battery at time t=0, so that a time-dependent current 11(t) starts following through the coil. If I2(t) is the current induced in the ring, and B (t) is the magnetic field at the axis of the coil due to I1(t) then as a function of time (t>0), the product I2(t)B(t)
increases with time
decreases with time
does not vary with time
passes through a maximum.
The correct Answer is:4
To solve the problem, we will follow these steps:
Step 1: Determine the Magnetic Field B(t)
The magnetic field B(t) at the axis of the coil due to the current I1(t) can be expressed as:
B(t)=μ0nI1(t)
where μ0 is the permeability of free space, n is the number of turns per unit length of the coil, and I1(t) is the time-dependent current flowing through the coil.
Step 2: Express the Current I1(t)
For a coil with inductance and resistance connected to a battery, the current I1(t) can be described by the equation:
I1(t)=I0(1−e−tτ)
where I0 is the maximum current, and τ is the time constant of the circuit.
Step 3: Substitute I1(t) into B(t)
Substituting I1(t) into the expression for B(t):
B(t)=μ0nI0(1−e−tτ)
Step 4: Calculate the Induced EMF E
The induced EMF E in the conducting ring is given by Faraday's law of electromagnetic induction:
E=−dΦdt
where Φ is the magnetic flux through the ring. The magnetic flux Φ can be expressed as:
Φ=B(t)⋅A
where A is the area of the ring. Thus,
E=−AdB(t)dt
Step 5: Differentiate B(t)
To find dB(t)dt:
dB(t)dt=μ0nI0ddt(1−e−tτ)=μ0nI0⋅1τe−tτ
Step 6: Substitute dB(t)dt into the EMF Equation
Substituting back into the EMF expression:
E=−A⋅μ0nI0⋅1τe−tτ
Step 7: Calculate the Induced Current I2(t)
The induced current I2(t) in the ring can be found using Ohm's law:
I2(t)=ER
where R is the resistance of the ring. Thus,
I2(t)=−Aμ0nI0Rτe−tτ
Step 8: Calculate the Product I2(t)B(t)
Now, we can find the product I2(t)B(t):
I2(t)B(t)=(−Aμ0nI0Rτe−tτ)(μ0nI0(1−e−tτ))
This simplifies to:
I2(t)B(t)=−Aμ20n2I20Rτe−tτ(1−e−tτ)
Step 9: Analyze the Behavior of I2(t)B(t)
As t→0, I2(t)B(t) approaches 0. As t→∞, I2(t)B(t) also approaches 0. Therefore, I2(t)B(t) will have a maximum value at some finite time t.
Conclusion
The product I2(t)B(t) passes through a maximum value at some point in time and returns to zero as t approaches infinity.
---
The magnetic field B(t) at the axis of the coil due to the current I1(t) can be expressed as:
B(t)=μ0nI1(t)
where μ0 is the permeability of free space, n is the number of turns per unit length of the coil, and I1(t) is the time-dependent current flowing through the coil.
For a coil with inductance and resistance connected to a battery, the current I1(t) can be described by the equation:
I1(t)=I0(1−e−tτ)
where I0 is the maximum current, and τ is the time constant of the circuit.
Substituting I1(t) into the expression for B(t):
B(t)=μ0nI0(1−e−tτ)
The induced EMF E in the conducting ring is given by Faraday's law of electromagnetic induction:
E=−dΦdt
where Φ is the magnetic flux through the ring. The magnetic flux Φ can be expressed as:
Φ=B(t)⋅A
where A is the area of the ring. Thus,
E=−AdB(t)dt
To find dB(t)dt:
dB(t)dt=μ0nI0ddt(1−e−tτ)=μ0nI0⋅1τe−tτ
Substituting back into the EMF expression:
E=−A⋅μ0nI0⋅1τe−tτ
The induced current I2(t) in the ring can be found using Ohm's law:
I2(t)=ER
where R is the resistance of the ring. Thus,
I2(t)=−Aμ0nI0Rτe−tτ
Now, we can find the product I2(t)B(t):
I2(t)B(t)=(−Aμ0nI0Rτe−tτ)(μ0nI0(1−e−tτ))
This simplifies to:
I2(t)B(t)=−Aμ20n2I20Rτe−tτ(1−e−tτ)
As t→0, I2(t)B(t) approaches 0. As t→∞, I2(t)B(t) also approaches 0. Therefore, I2(t)B(t) will have a maximum value at some finite time t.
The product I2(t)B(t) passes through a maximum value at some point in time and returns to zero as t approaches infinity.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 110videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 210videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )31videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
Similar Questions
Knowledge Check
- Question 1 - Select One
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 Nm
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
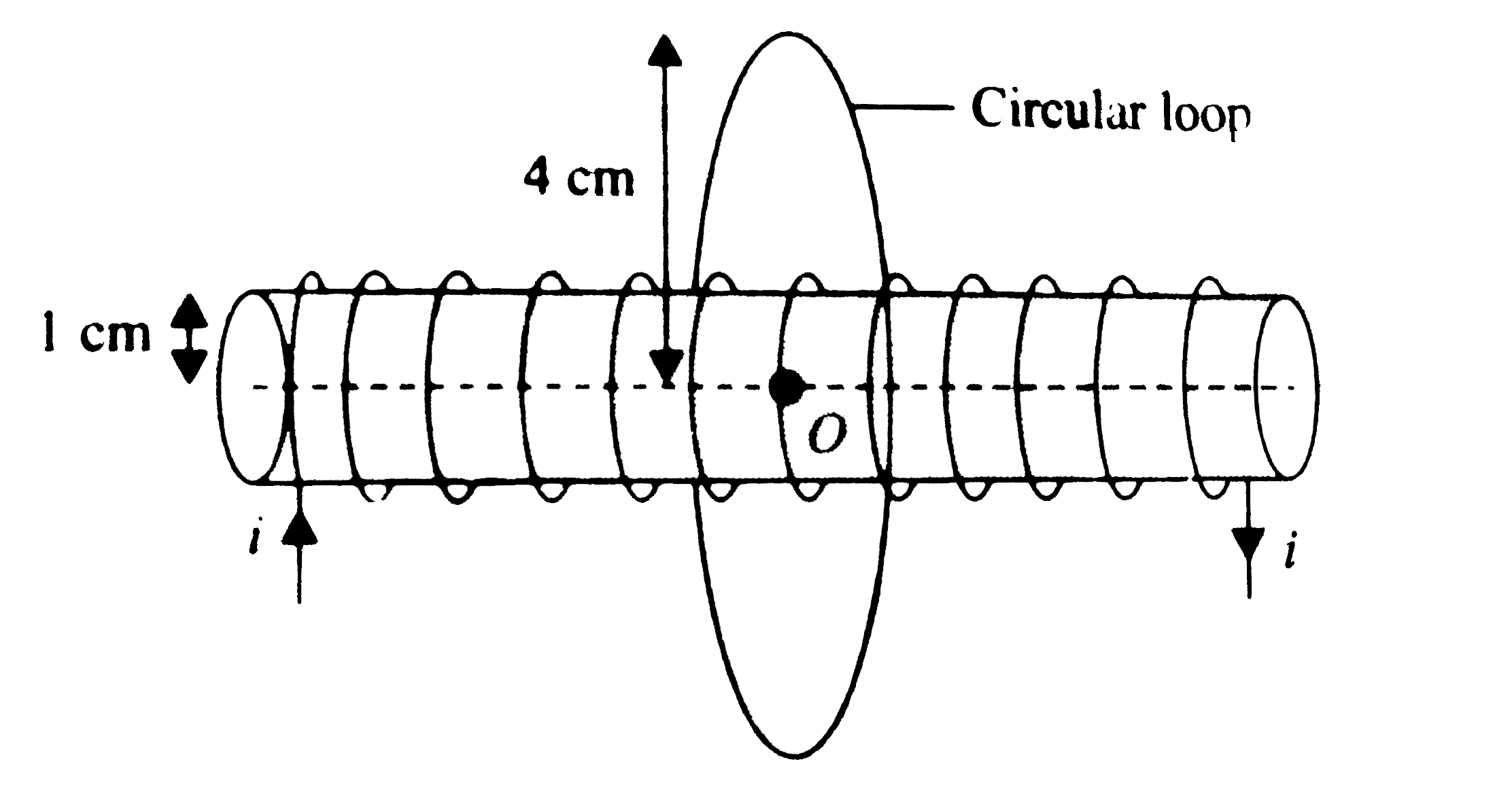
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centreView SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
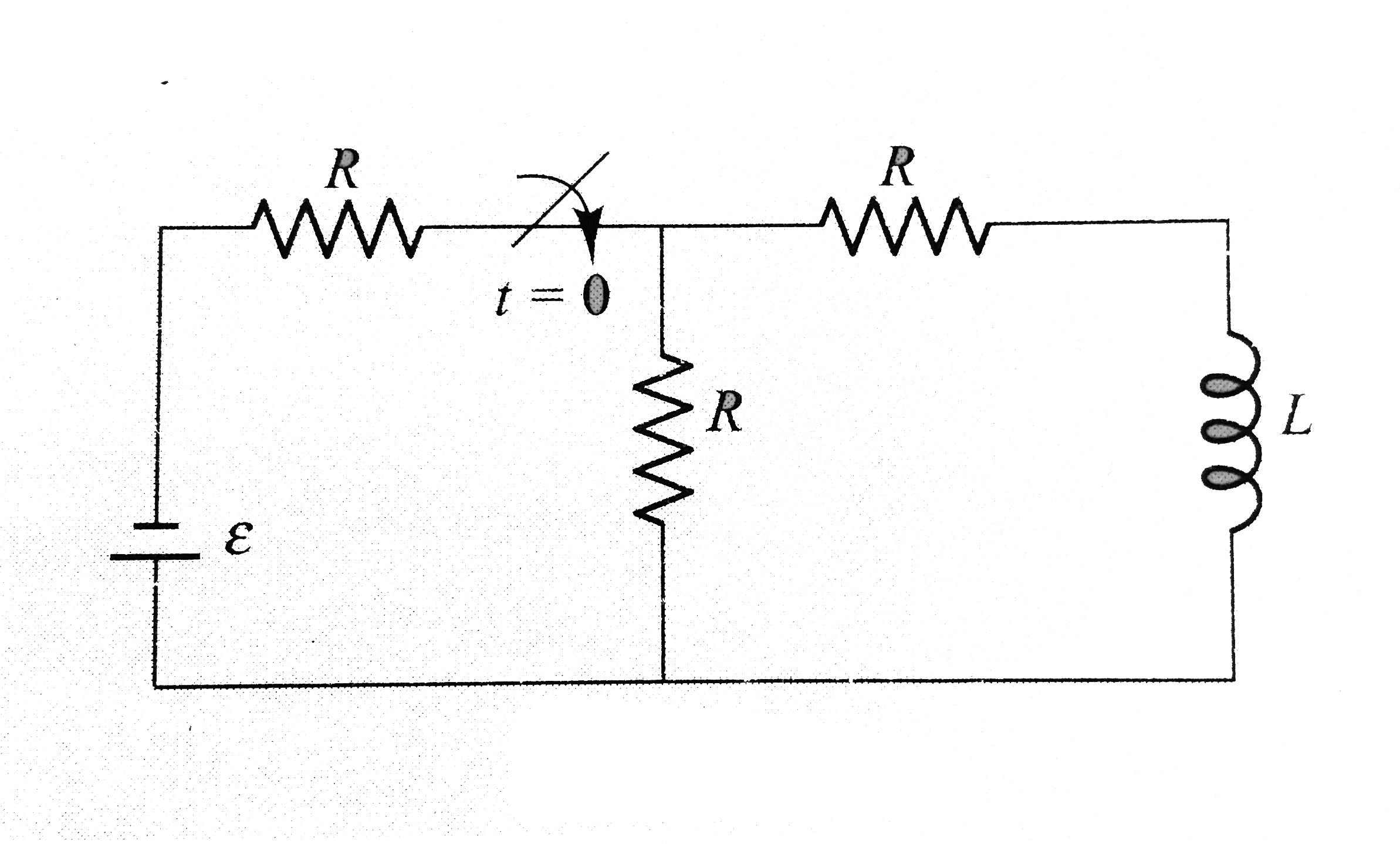 View Solution
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA coil having inductance and L and resistance R is connected to a battery of emf ∈ at t=0. If t1 and t2 are time for 90% and 99% completion of current growth in the circuit, then t1t2 will be-
View SolutionThe current in the inner coil is I=2t2. Find the heat developed in the outer coil between t =0 and t seconds. The resistance of the outer coil is R and take b>>a.
 View Solution
View SolutionA coil of inductanece 5H is joined to a cell of emf 6V through a resistance 10Ω at time t=0. The emf across the coil at time t=ln√2 s is:
View SolutionIn the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
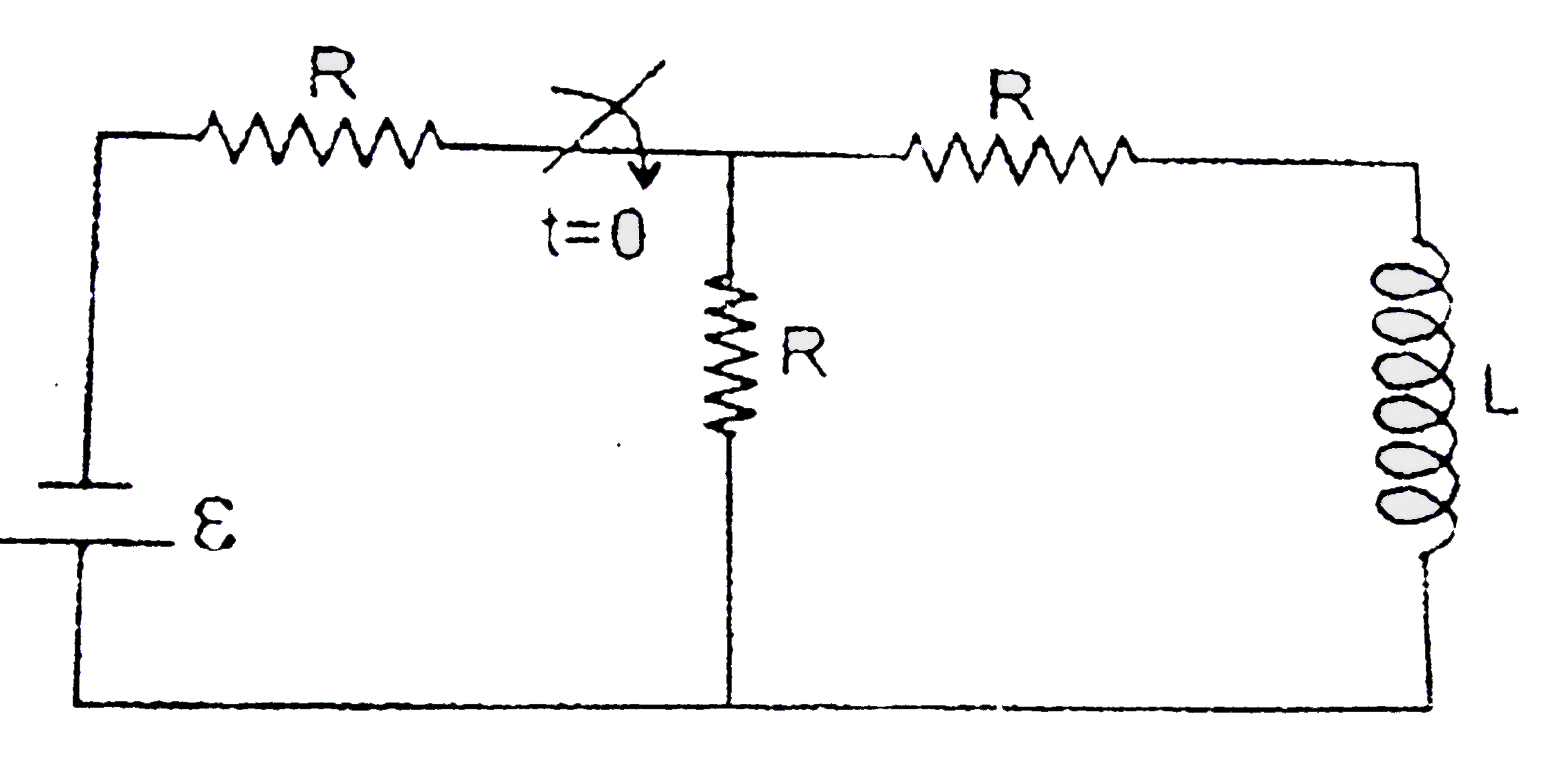 View Solution
View Solution
