Calculate the self inductance per unit length of a current loop formed by joining the ends of two long parallel wires of radius r separated by a distance d between their axes, neglecting the end effects and magnetic flux within the wires.
To calculate the self-inductance per unit length of a current loop formed by joining the ends of two long parallel wires, we can follow these steps:
Step 1: Understanding the Configuration
We have two long parallel wires with radius r and separated by a distance d between their axes. We will neglect the end effects and the magnetic flux within the wires.
Step 2: Magnetic Field Calculation
The magnetic field B at a distance x from one wire (due to that wire) is given by:
B=μ0I2πx
where μ0 is the permeability of free space and I is the current flowing through the wire.
For the second wire, the distance from the center is d−x, so the magnetic field due to the second wire is:
B′=μ0I2π(d−x)
Step 3: Total Magnetic Field
The total magnetic field Bnet in the region between the two wires is the sum of the magnetic fields due to both wires:
Bnet=B+B′=μ0I2πx+μ0I2π(d−x)
Step 4: Magnetic Flux Calculation
The magnetic flux Φ through an elemental strip of width dx and length L is given by:
dΦ=Bnet⋅dA=Bnet⋅(L⋅dx)
Substituting for Bnet:
dΦ=(μ0I2πx+μ0I2π(d−x))Ldx
Step 5: Integrating to Find Total Flux
To find the total magnetic flux Φ, we integrate dΦ from x=r to x=d−r:
Φ=∫d−rrdΦ=∫d−rr(μ0I2πx+μ0I2π(d−x))Ldx
Step 6: Solving the Integral
Calculating the integral:
Φ=μ0IL2π(∫d−rr1xdx+∫d−rr1d−xdx)
The integrals evaluate to:
∫1xdx=lnxand∫1d−xdx=−ln(d−x)
Thus,
Φ=μ0IL2π(ln(d−r)−ln(r)+ln(d−r)−ln(r))
This simplifies to:
Φ=μ0IL2π(2ln(d−rr))
Step 7: Finding Self-Inductance
Using the relation Φ=LI, we can express the self-inductance L:
L=ΦI=μ0Lπln(d−rr)
Step 8: Self-Inductance per Unit Length
To find the self-inductance per unit length, we divide L by L:
LL=μ0πln(d−rr)
Final Result
The self-inductance per unit length of the current loop is:
LL=μ0πln(d−rr)
We have two long parallel wires with radius r and separated by a distance d between their axes. We will neglect the end effects and the magnetic flux within the wires.
The magnetic field B at a distance x from one wire (due to that wire) is given by:
B=μ0I2πx
where μ0 is the permeability of free space and I is the current flowing through the wire.
B′=μ0I2π(d−x)
The total magnetic field Bnet in the region between the two wires is the sum of the magnetic fields due to both wires:
Bnet=B+B′=μ0I2πx+μ0I2π(d−x)
The magnetic flux Φ through an elemental strip of width dx and length L is given by:
dΦ=Bnet⋅dA=Bnet⋅(L⋅dx)
Substituting for Bnet:
dΦ=(μ0I2πx+μ0I2π(d−x))Ldx
To find the total magnetic flux Φ, we integrate dΦ from x=r to x=d−r:
Φ=∫d−rrdΦ=∫d−rr(μ0I2πx+μ0I2π(d−x))Ldx
Calculating the integral:
Φ=μ0IL2π(∫d−rr1xdx+∫d−rr1d−xdx)
The integrals evaluate to:
∫1xdx=lnxand∫1d−xdx=−ln(d−x)
Thus,
Φ=μ0IL2π(ln(d−r)−ln(r)+ln(d−r)−ln(r))
This simplifies to:
Φ=μ0IL2π(2ln(d−rr))
Using the relation Φ=LI, we can express the self-inductance L:
L=ΦI=μ0Lπln(d−rr)
To find the self-inductance per unit length, we divide L by L:
LL=μ0πln(d−rr)
The self-inductance per unit length of the current loop is:
LL=μ0πln(d−rr)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - SOLVED EXAMPLES
24 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 1
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
Knowledge Check
Find the inductance of a unit length of two parallel wires, each of radius a, whose centers are a distance d apart and carry equal currents in opposite direction. Neglect the flux within the wire.
Aμ02πIn(d−aa)Bμ0πIn(d−aa)C3μ0πIn(d−aa)D3μ03πIn(d−aa)
Consider the self-inductance per unit length of a solenoid at its centre and that near its ends. Which of the two is greater?
View SolutionCalculate the force per unit length on a long straight wire carrying current 4A due to parallel wire carrying current 6A current. Distance between the wires =3cm.
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionTwo long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionThe wire loop PQRSP formed by joining two semicircular wires of radii R1 and R2 carries a current I as shown . The magnitude of the magnetic induction at the center C is ………..
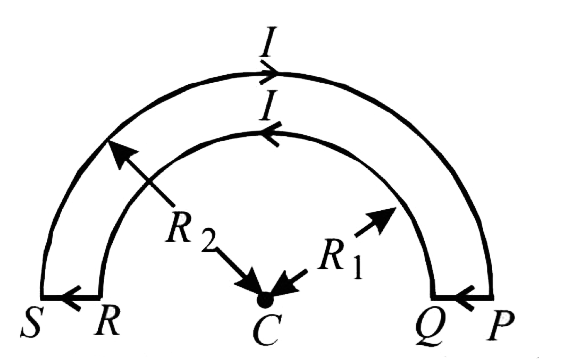
View SolutionThe wire loop PQRSP formed by joining two semicircular wires of radii R1 and R2 carries a current I as shown. The magnitude of the magnetic induction at the centre C is ____________.

View Solution
