Considering the earth as a short magnet with its centre coinciding with the centre of earth, show that the angle of dip ϕ is related to magnetic latitude λ through the relation tanϕ=2tanλ
To show that the angle of dip ϕ is related to the magnetic latitude λ through the relation tanϕ=2tanλ, we can follow these steps:
Step 1: Understanding the Earth as a Magnet
Consider the Earth as a short magnet with its center coinciding with the center of the Earth. The magnetic field lines emerge from the North Pole and enter at the South Pole. The angle of dip ϕ is the angle made by the resultant magnetic field with the horizontal plane.
Step 2: Define Magnetic Latitude
The magnetic latitude λ is defined as the angle between the magnetic equator (where the magnetic field is horizontal) and the location of interest on the Earth's surface.
Step 3: Components of the Magnetic Field
At any point on the Earth's surface, the magnetic field can be resolved into two components:
- The vertical component Bv
- The horizontal component Bh
The angle of dip ϕ can be expressed as:
tanϕ=BvBh
Step 4: Magnetic Field Components
For a magnetic dipole (like Earth), the magnetic field components can be expressed as:
- The vertical component Bv at a point is proportional to the cosine of the angle θ (where θ is the angle from the magnetic axis).
- The horizontal component Bh is proportional to the sine of the angle θ.
Thus, we can write:
Bv=2kcosθ
Bh=ksinθ
where k is a constant related to the magnetic moment of the Earth.
Step 5: Substitute Components into the Tangent Expression
Substituting the expressions for Bv and Bh into the tangent expression gives:
tanϕ=BvBh=2kcosθksinθ=2cosθsinθ=2cotθ
Step 6: Relate θ to λ
From geometry, we know that:
θ=90∘+λ
Thus, we can substitute θ into our expression for tanϕ:
tanϕ=2cot(90∘+λ)
Step 7: Simplify Using Trigonometric Identities
Using the identity cot(90∘+x)=−tanx:
tanϕ=2(−tanλ)=−2tanλ
Since we are interested in the magnitude, we can express it as:
tanϕ=2tanλ
Conclusion
Thus, we have shown that:
tanϕ=2tanλ
Consider the Earth as a short magnet with its center coinciding with the center of the Earth. The magnetic field lines emerge from the North Pole and enter at the South Pole. The angle of dip ϕ is the angle made by the resultant magnetic field with the horizontal plane.
The magnetic latitude λ is defined as the angle between the magnetic equator (where the magnetic field is horizontal) and the location of interest on the Earth's surface.
At any point on the Earth's surface, the magnetic field can be resolved into two components:
- The vertical component Bv
- The horizontal component Bh
tanϕ=BvBh
For a magnetic dipole (like Earth), the magnetic field components can be expressed as:
- The vertical component Bv at a point is proportional to the cosine of the angle θ (where θ is the angle from the magnetic axis).
- The horizontal component Bh is proportional to the sine of the angle θ.
Bv=2kcosθ
Bh=ksinθ
where k is a constant related to the magnetic moment of the Earth.
Substituting the expressions for Bv and Bh into the tangent expression gives:
tanϕ=BvBh=2kcosθksinθ=2cosθsinθ=2cotθ
From geometry, we know that:
θ=90∘+λ
Thus, we can substitute θ into our expression for tanϕ:
tanϕ=2cot(90∘+λ)
Using the identity cot(90∘+x)=−tanx:
tanϕ=2(−tanλ)=−2tanλ
Since we are interested in the magnitude, we can express it as:
tanϕ=2tanλ
Thus, we have shown that:
tanϕ=2tanλ
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:SOLVED EXAMPLES
Explore 20 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:PRACTICE EXERCISE 1
Explore 1 Video
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IMPECCABLE
Explore 53 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
Similar Questions
A vertical circular coil of one turn and radius 9.42 cm is placed with its plane in the magnetic meridian and short magnetic needle is pivoted at the centre of the coil so that it can freely rotate in the horizontal plane. If a current of 6A is passed through the coil, then the needle deflects by (BH=4×10−5T)
View SolutionLet the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator
View Solution
Knowledge Check
Let the magnetic field on earth be modeled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator is
Aalways zeroBpositive, negative or zeroCunboundedDalways negativeAssertion : The magnetic Held lines of the earth resemble that of a magnetic dipole located at the centre of the earth.
Reason : The axis of the dipole coincide with the axis of rotation of the earth.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is ture but reason is false.DIf both assertion and reason are false.Consider the plane S formed by the dipole axis and the axis of earth. Let P be point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators Obtain the declination and dip angles at P and Q.
A0∘,11.3∘B11.3∘,0∘C11.3∘,11.3∘D0∘,0∘
A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north south direction. Null points are found on the axis of the magnet at 14cm from the centre of the magnet. The earth's magnetic field at the plane is 0⋅36G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null points (i.e. 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and apposite to the horizontal component of earth's magnetic field).
View SolutionTwo coils each of 100 turns are held such that one lies in vertical plane and the other in the horizontal plane with their centres coinciding. The radius of the vetical coil is 0.20m and that of the horizontal coil is 0.30m. How will you neutralize the magnetic field of the earth at their common centre? What is the current to be passed through each coil? Horizontal component of earth's magnetic field =0.35×10−4T and angle of dip =30∘.
View SolutionConsider the plane S formed by the dipole axis and the axis of earth. Let P be point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators Obtain the declination and dip angles at P and Q.
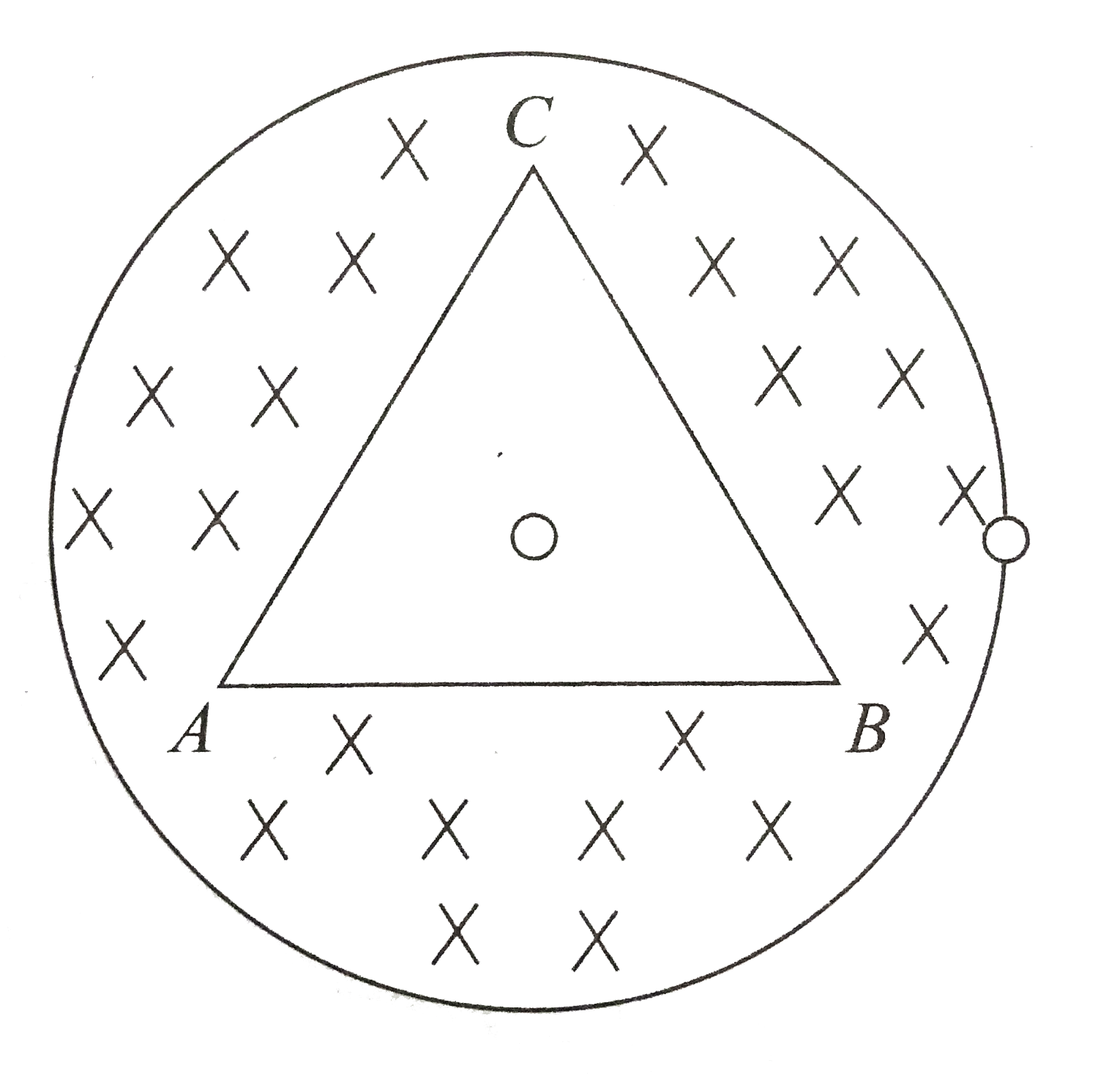
View SolutionA triangular wire frame (each side =2m) is placed in a region of time variant magnetic field dB/dt=(√3)T/s. The magnetic field is perpendicular to the plane of the triangle and its centre coincides with the centre of triangle. The base of the triangle AB has a resistance 1(Ω) while the other two sides have resistance 2(Ω) each. The magnitude of potential difference between the points A and B will be
View Solution(1) Centre of gravity (C.G.) of a body is the point at which the weight of the body acts,
(2) Centre of mass coincides with the centre of gravity if the earth is assumed to have infinitely large radius,
(3) To evaluate the gravitational field intensity due to any body at an external point, the entire mass of the body can be considered to be concentrated at its C.G..,
(4) The radius of gyration of any body rotating about an axis is the length of the perpendicular dropped from the C.G. of the body to the axis. which one of the following pairs of statements is correct ?
View Solution