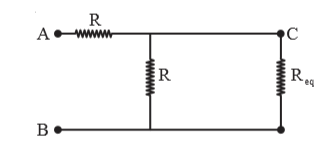
The equivalent resistance between points A and B of an infinite network of resistance each of 1Ω connected as shown is
A
infinite
B
2Ω
C
1+√52Ω
D
zero
Video Solution
Text Solution
The correct Answer is:C
Req=R+(RIIReq)=R+ReqR+Req ⇒ Req=12[1+√5]Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:PRACTICE EXERCISE-1
Explore 5 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:PRACTICE EXERCISE-2
Explore 5 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 48
Explore 1 Video
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
Similar Questions
Knowledge Check
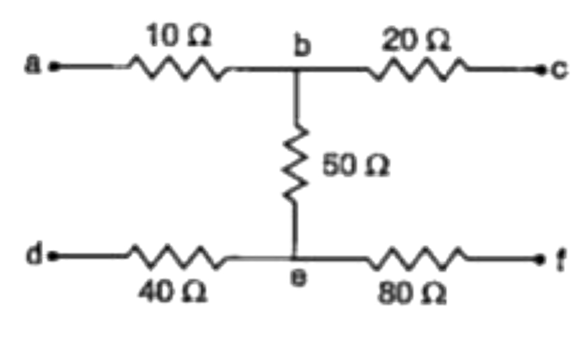
The equivalent resistance between points a and f of the network shown in figure below is
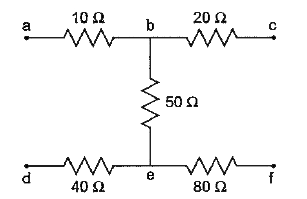 A24ΩB110ΩC140ΩD200Ω
A24ΩB110ΩC140ΩD200Ω
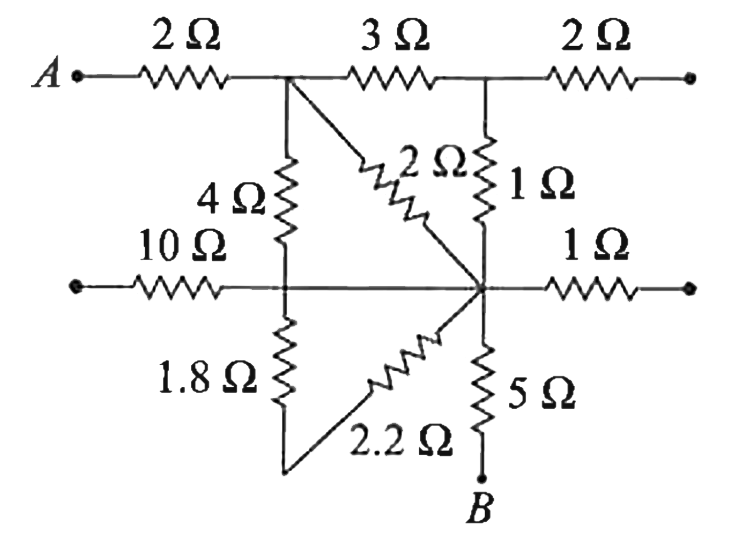
Equivalent resistance between the points A and B (in Ω)
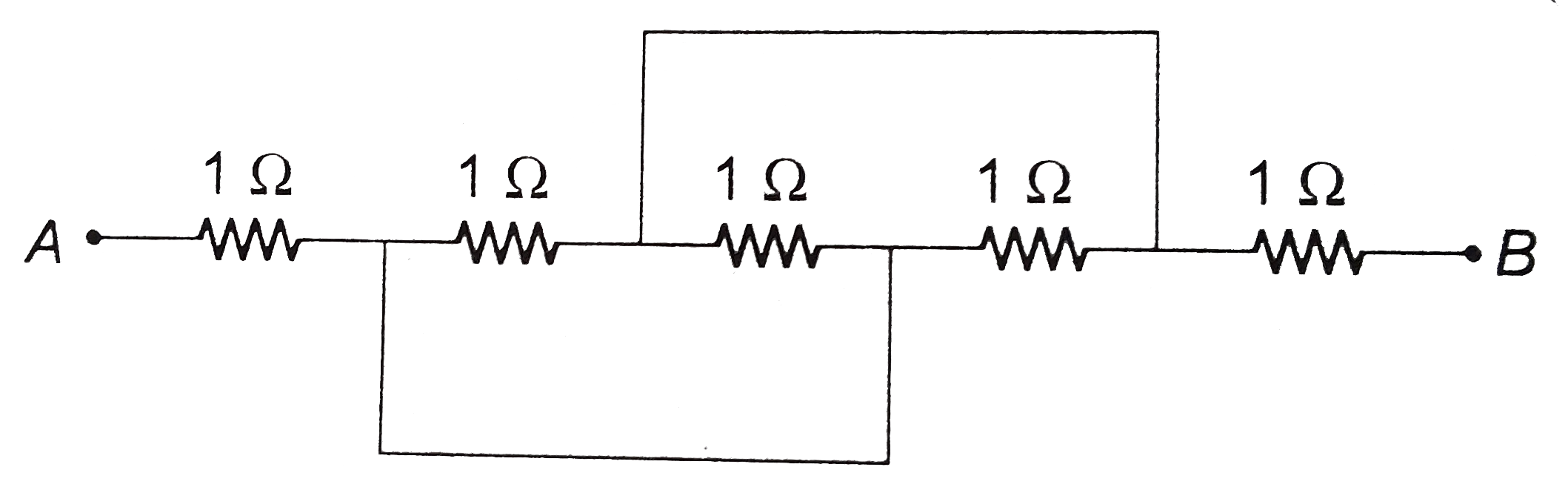 .
.
View SolutionThe equivalent resistance between A and B in the arrangement of resistance as shown is
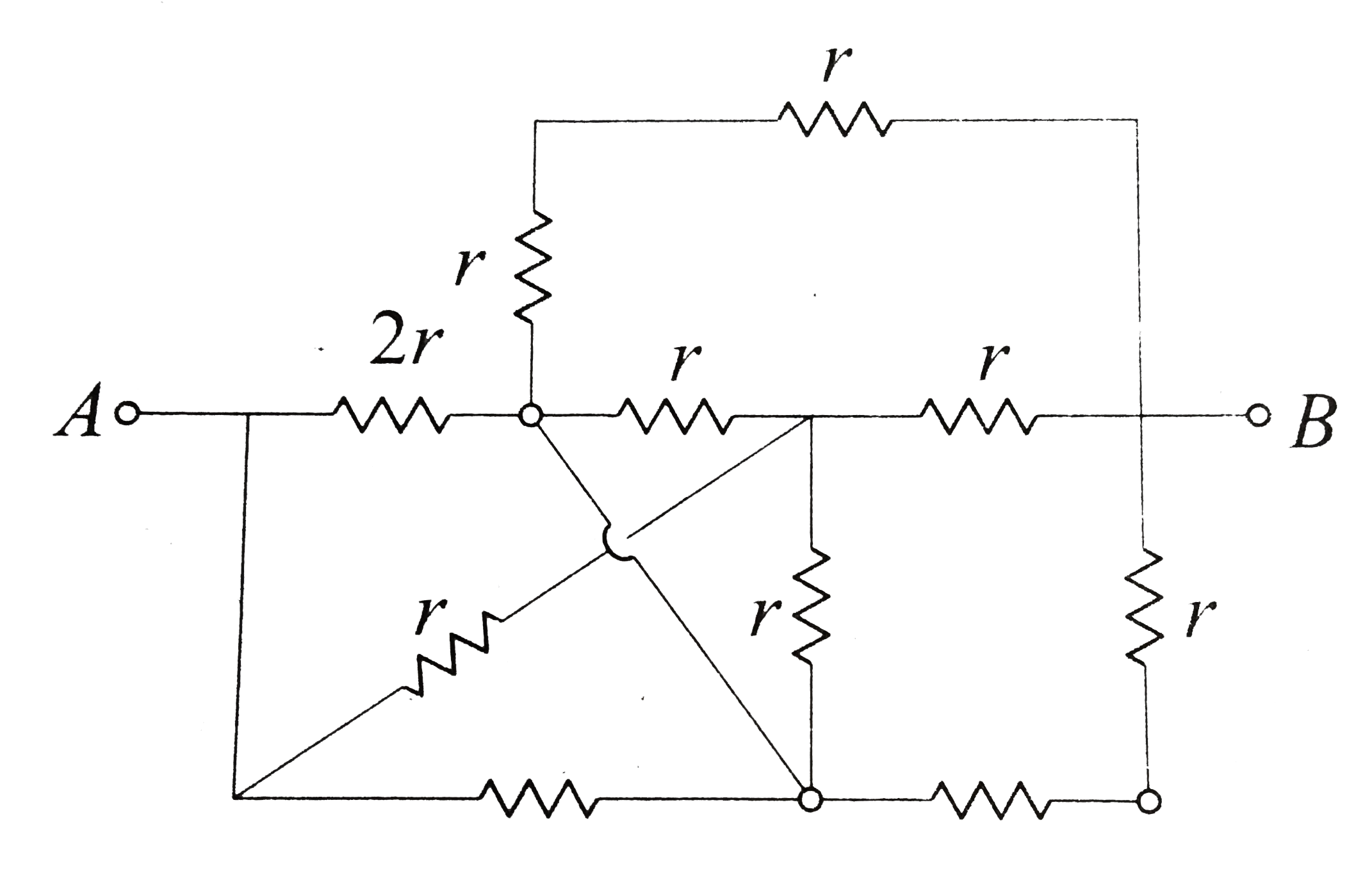
View SolutionThe equivalen resistance between A and B in the network shown in figure is
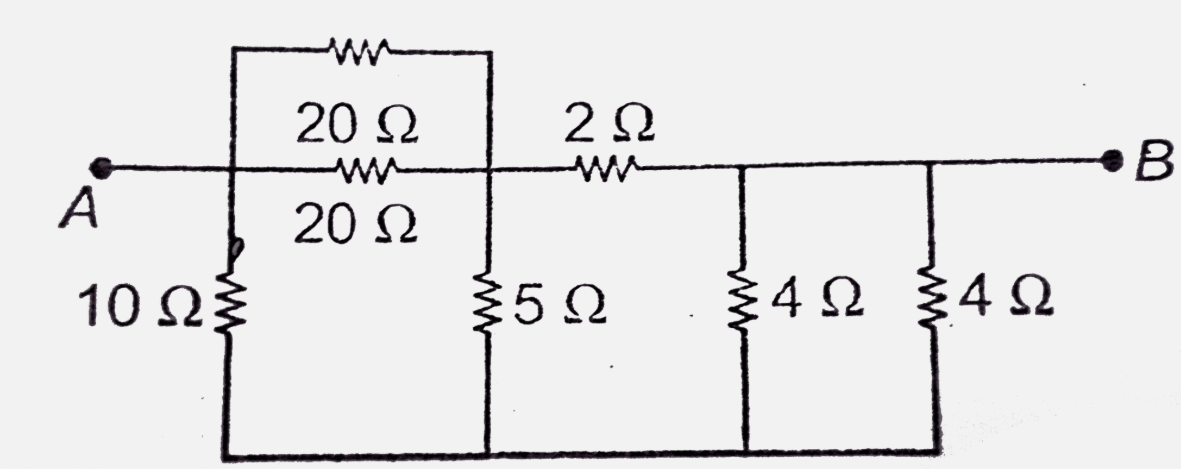
View SolutionFind the equivalent resistance between the points a and c of the given network for resistors
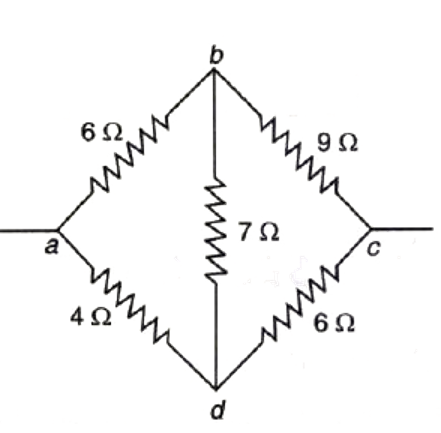
View SolutionThe equivalent resistance between A and B will be (in Ω)
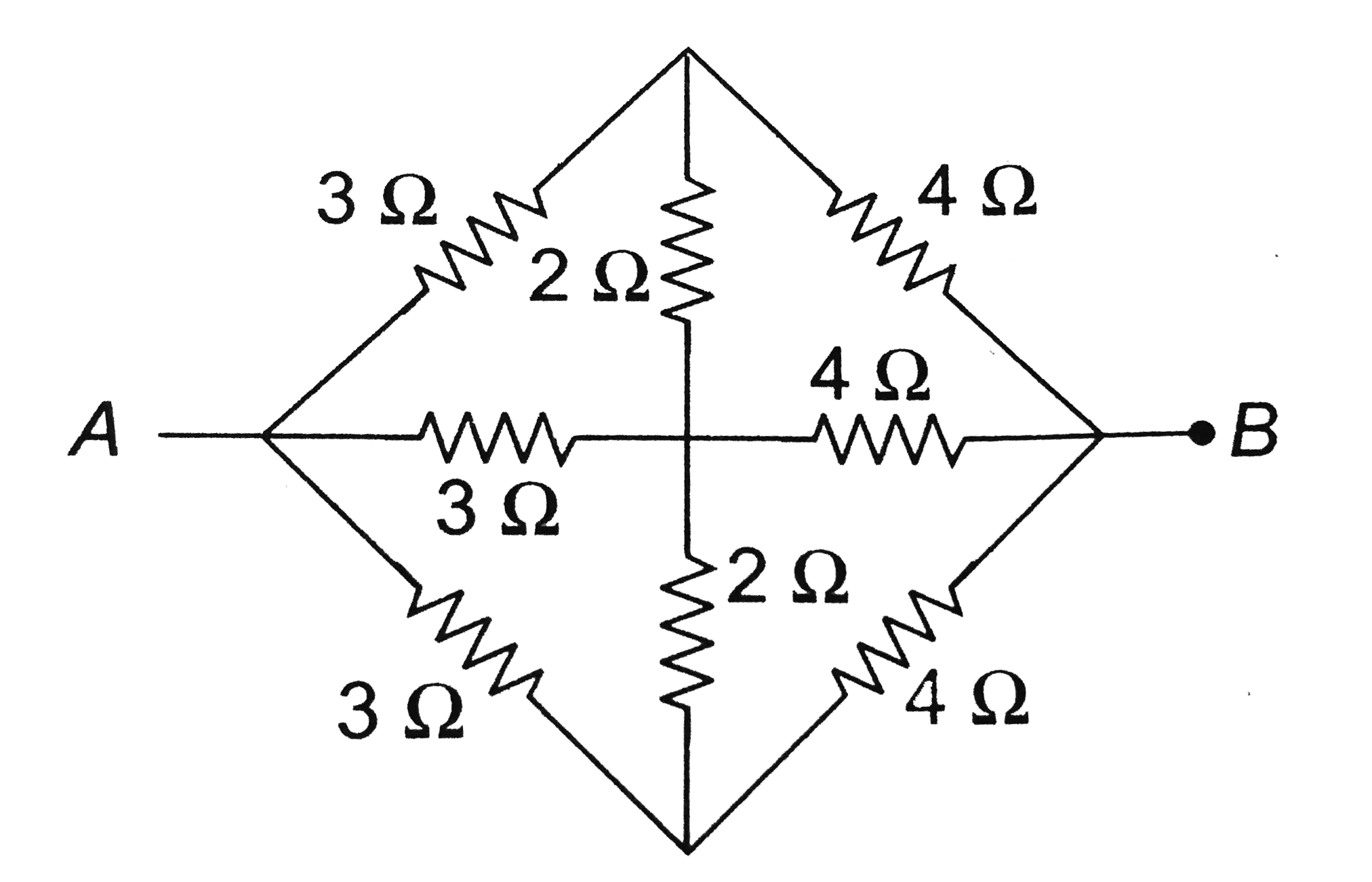
View SolutionThe equivalent resistance between the points A and B will be (each resistance is 15Ω)
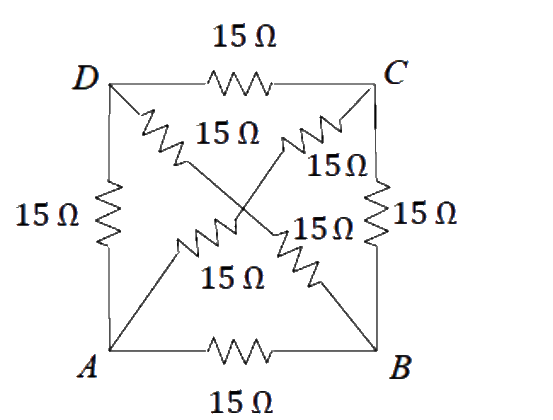
View SolutionThe equivalent resistance between the point A and B will be : (each resistance is 15Ω )
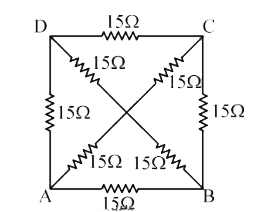
View Solution