In a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have a metre bridge where the null point is initially found at a distance of 35 cm from point A. When a resistance of 10 Ω is connected in parallel with the unknown resistance S, the null point shifts to 50 cm.
Step 2: Use the metre bridge formula
The formula for the metre bridge is given by:
S=100−LL×R
where:
- S is the unknown resistance,
- L is the balancing length,
- R is the known resistance.
Step 3: Calculate S using the first condition
From the first condition, where the null point is at 35 cm:
S=100−3535×R
S=6535×R
S=137R(Equation 1)
Step 4: Set up the equation for the second condition
When a 10 Ω resistance is connected in parallel with S, the new equivalent resistance S′ can be calculated as:
1S′=1S+110
This can be rearranged to:
S′=10SS+10
Step 5: Calculate S' using the second condition
From the second condition, where the null point is now at 50 cm:
S′=100−5050×R
S′=5050×R
S′=R(Equation 2)
Step 6: Equate the two expressions for S'
From Equation 2, we have:
R=10SS+10
Step 7: Substitute Equation 1 into the new equation
Substituting S=137R into the equation R=10SS+10:
R=10(137R)(137R)+10
Step 8: Simplify the equation
Cross-multiplying gives:
R(137R+10)=130R
137R2+10R=130R
137R2−120R=0
Factoring out R:
R(137R−120)=0
So, either R=0 (not possible) or:
137R=120
R=120×713
R=84013≈64.62Ω
Step 9: Calculate S using R
Now substituting R back into Equation 1:
S=137R=137×84013=120Ω
Final Values
Thus, the values of the resistances are:
- R≈64.62Ω
- S=120Ω
We have a metre bridge where the null point is initially found at a distance of 35 cm from point A. When a resistance of 10 Ω is connected in parallel with the unknown resistance S, the null point shifts to 50 cm.
The formula for the metre bridge is given by:
S=100−LL×R
where:
- S is the unknown resistance,
- L is the balancing length,
- R is the known resistance.
From the first condition, where the null point is at 35 cm:
S=100−3535×R
S=6535×R
S=137R(Equation 1)
When a 10 Ω resistance is connected in parallel with S, the new equivalent resistance S′ can be calculated as:
1S′=1S+110
This can be rearranged to:
S′=10SS+10
From the second condition, where the null point is now at 50 cm:
S′=100−5050×R
S′=5050×R
S′=R(Equation 2)
From Equation 2, we have:
R=10SS+10
Substituting S=137R into the equation R=10SS+10:
R=10(137R)(137R)+10
Cross-multiplying gives:
R(137R+10)=130R
137R2+10R=130R
137R2−120R=0
Factoring out R:
R(137R−120)=0
So, either R=0 (not possible) or:
137R=120
R=120×713
R=84013≈64.62Ω
Now substituting R back into Equation 1:
S=137R=137×84013=120Ω
Thus, the values of the resistances are:
- R≈64.62Ω
- S=120Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - SOLVED EXAMPLES
24 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-1
5 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Video
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
In a meter bridge,
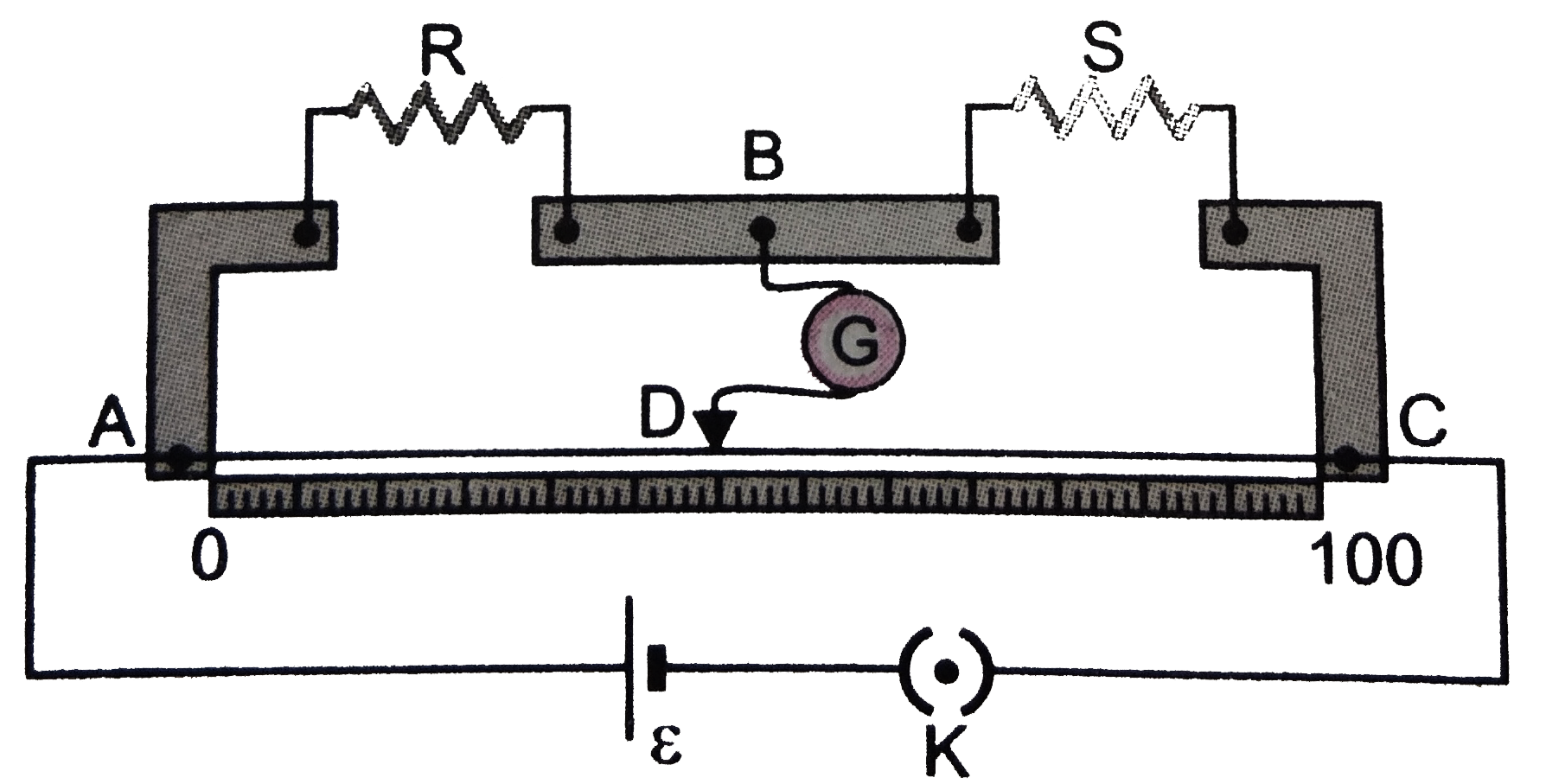
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionIn a meter bridge, the null point is found at a distance of l1cm from A. if now a resistance of X is connected in parallel with S, the null point occurs at l2cm. Obtain a formula for X is terms of l1,l2andS.
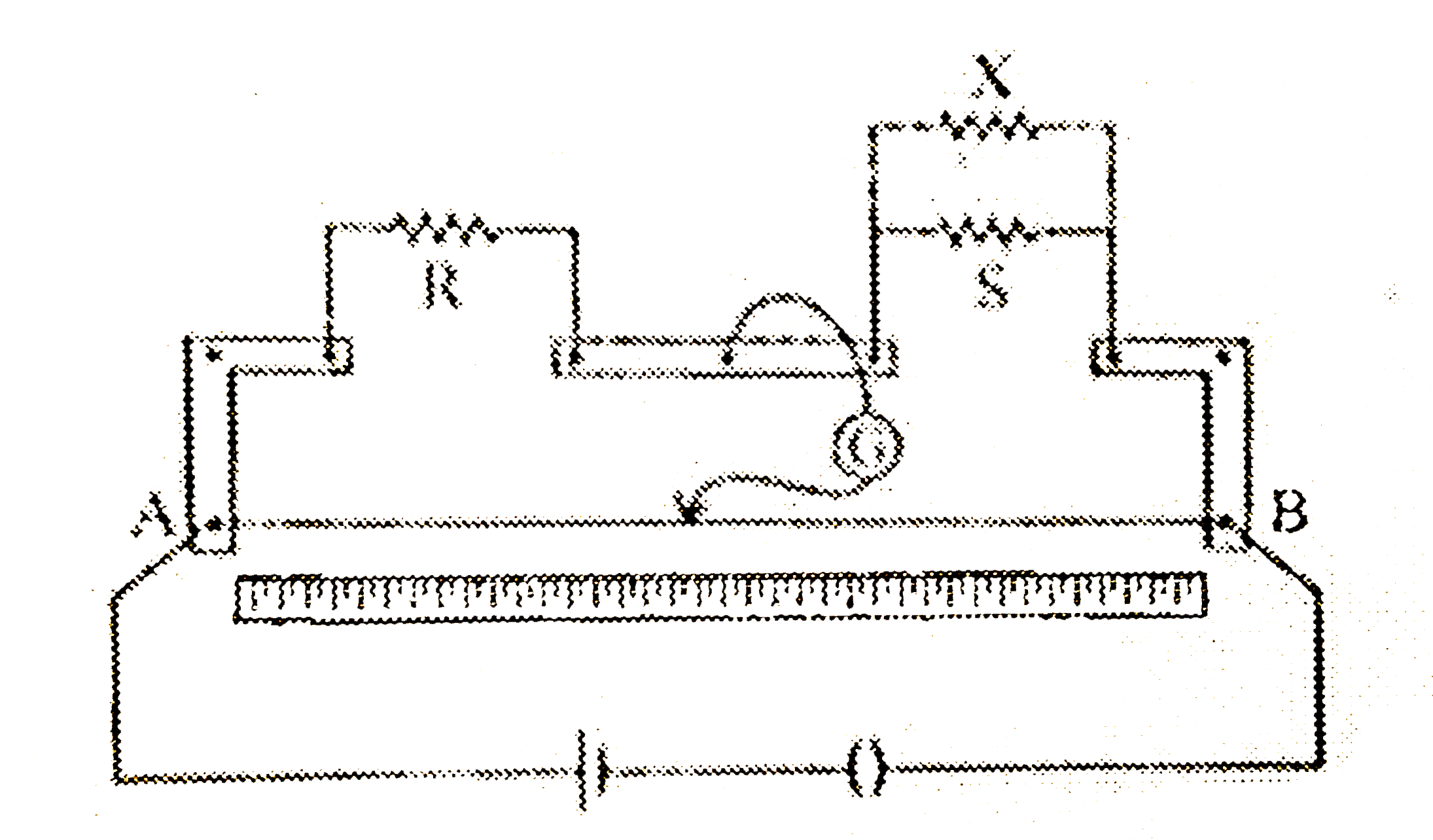
View SolutionCircuit diagram of metre bridge is shown in figure. The null point is found at a distance of 40cm from A. it now a resistance of 12Ω is connected in parallel with S, the null point occurs at 64cm.

View SolutionIn the experimental set up of meter bridge shown in the figure, the null point is obtained at a distance of 40 cm from A. If a 10Ω resistance is connected in series with R1, the null point shifts by 10 cm. The resistance that should be connected in parallel with (R1+10)Ω such that the null point shifts back to its initial position is :
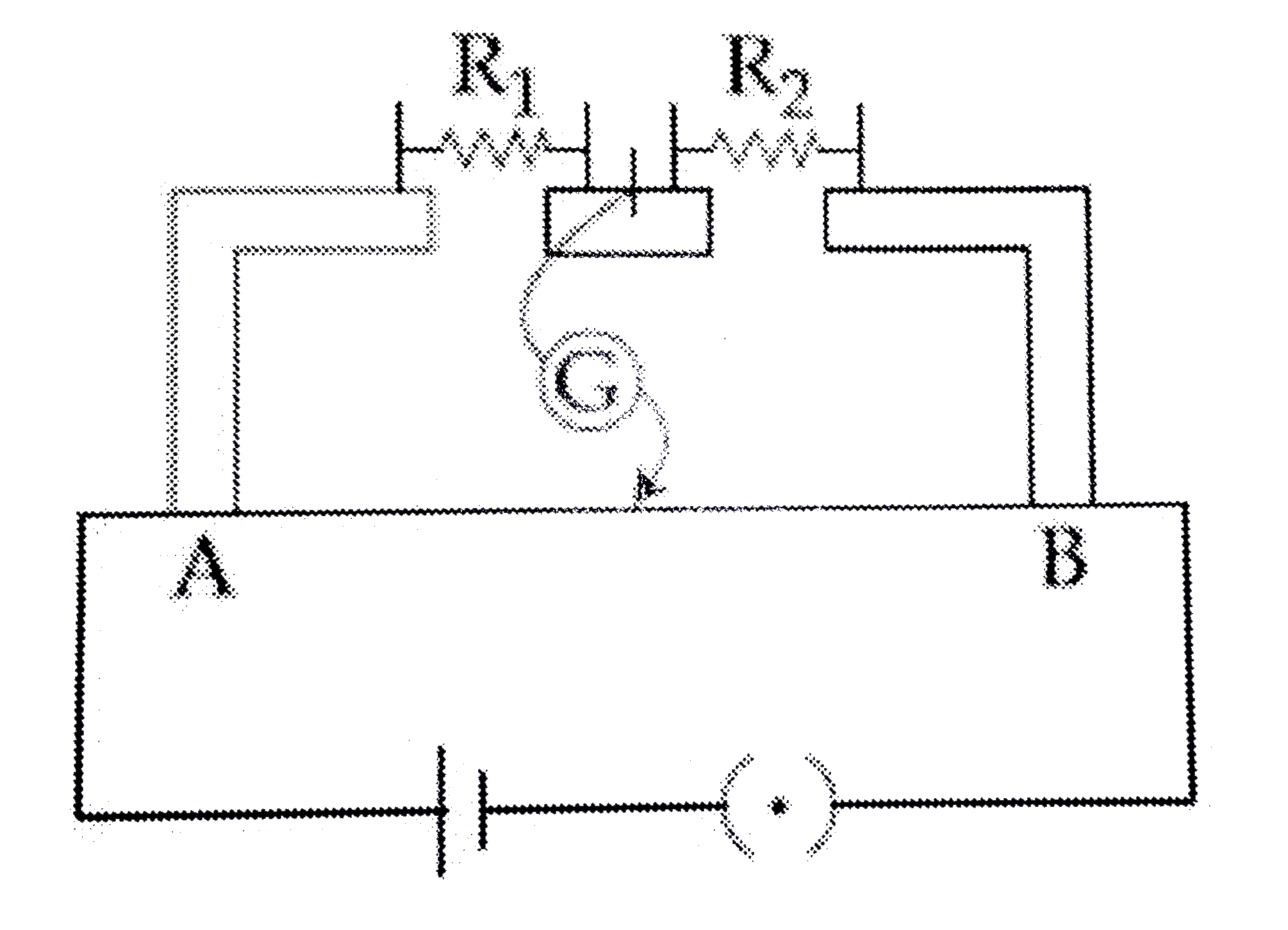
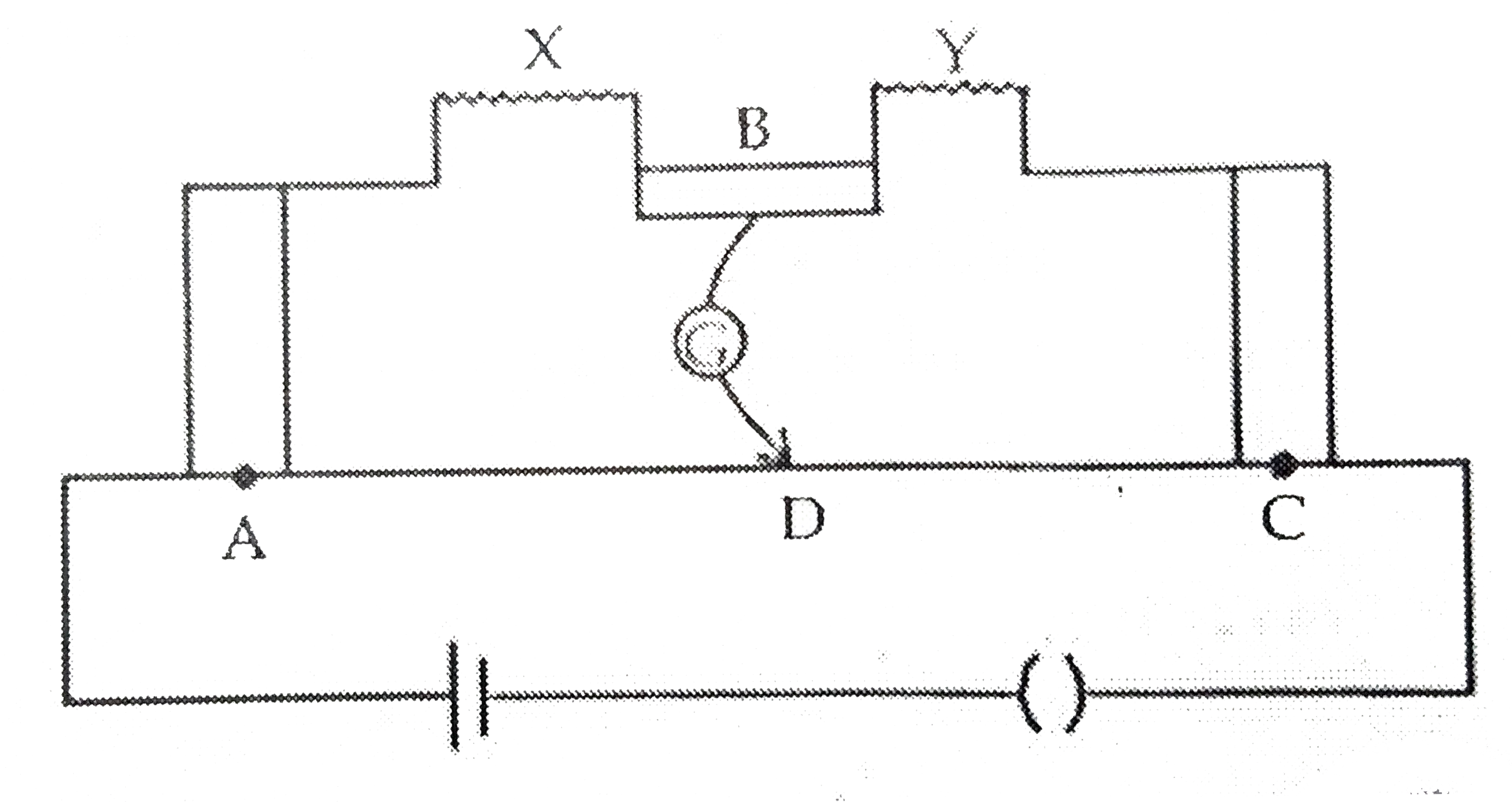
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View SolutionTwo unknown resistances X and Y are placed on the left and right gaps of a meter bridge. The null point in the galvanometer is obtained at a distance of 80cm from left. A resistance of 100Ω is now connected in parallel across X. The null point is then found by shifting the sliding contact toward left by 20cm. Calculate X and Y.
View SolutionIn the meter bridge experimental set up, shown in the figure, the null point 'D' is obtained at a distance of 40 cm from end A of the meter bridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD=60cm. Calculate the values of R1andR2.

View SolutionThe figure
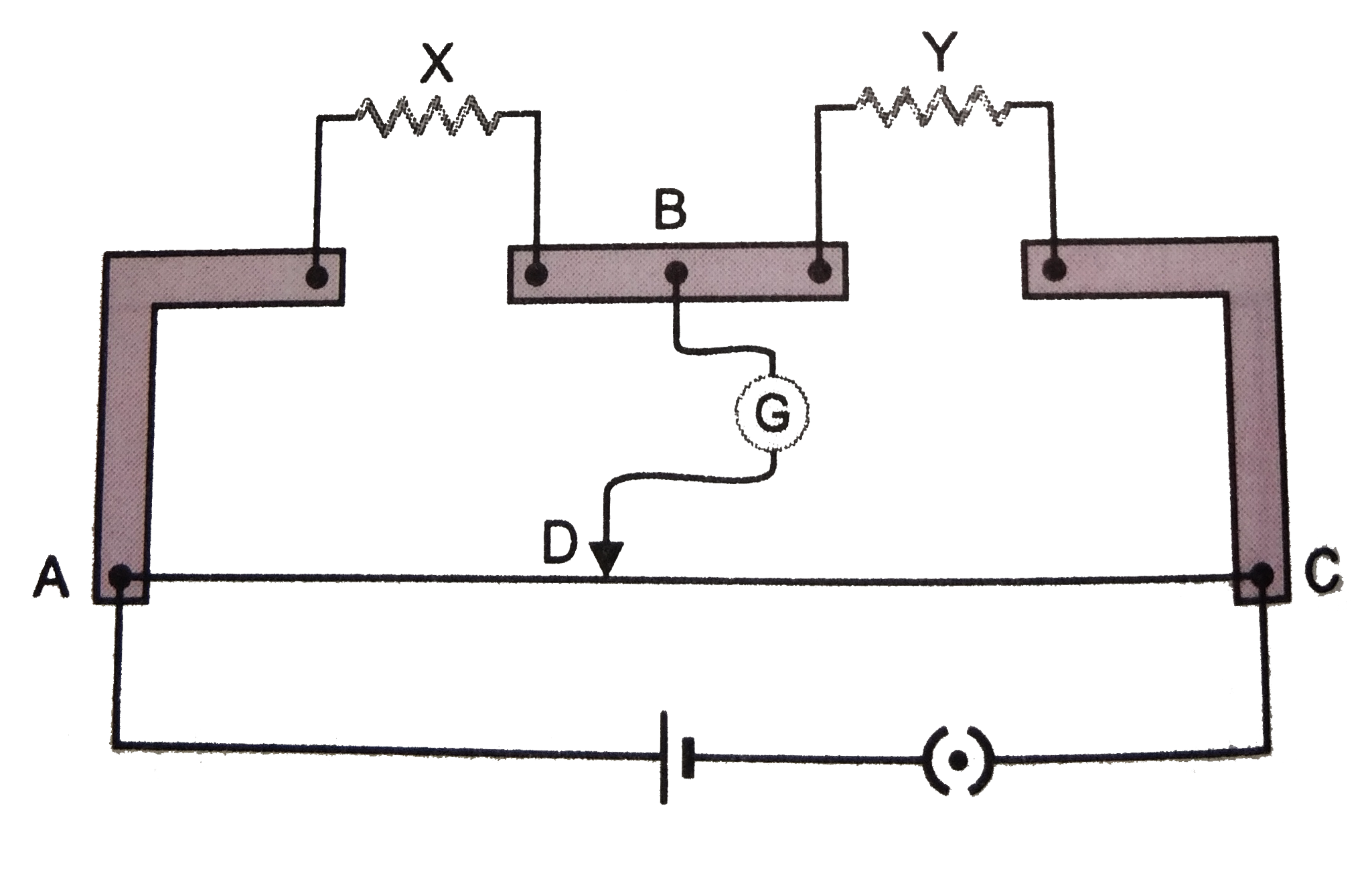
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.
View Solution
