Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then
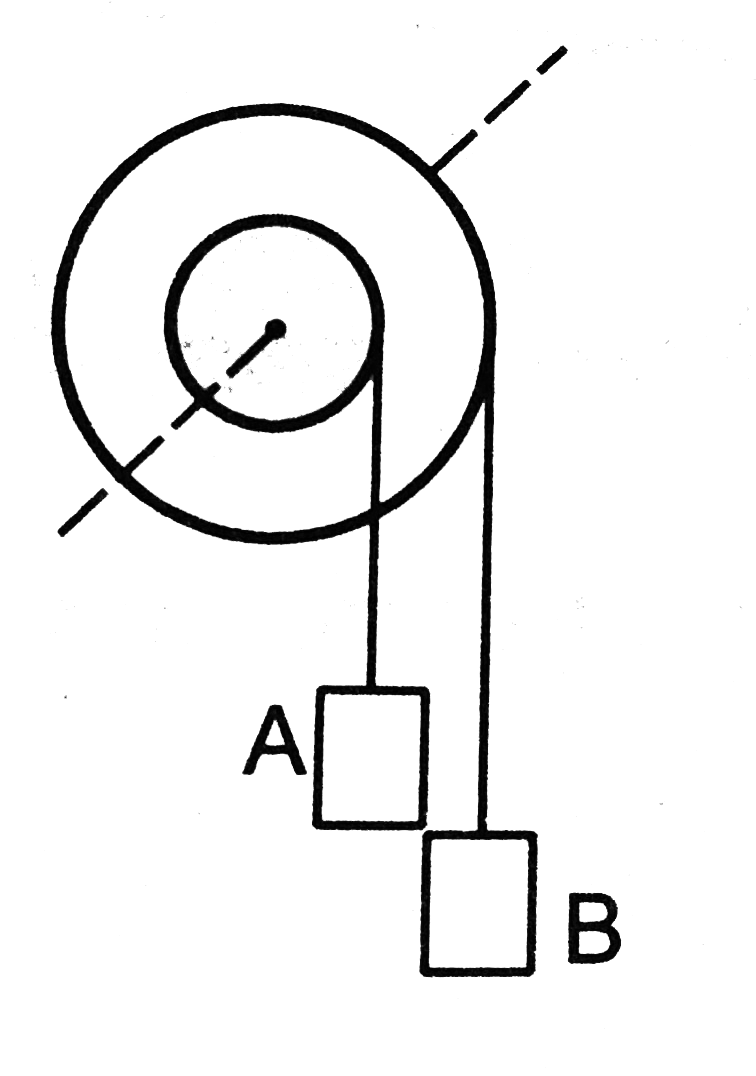
Linear displacement (S) = Radius (r) x Angular displacement (θ) ∵ S ∝ r(if θ constant) Distance travelled by mass A(x) /Distance travelled by mass B( y)= Radius of pulley concerned with mass A( r )/Radius of pulley concerned with mass B(2r )=1/2 ⇒y=2x.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-3
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-4
7 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
figure
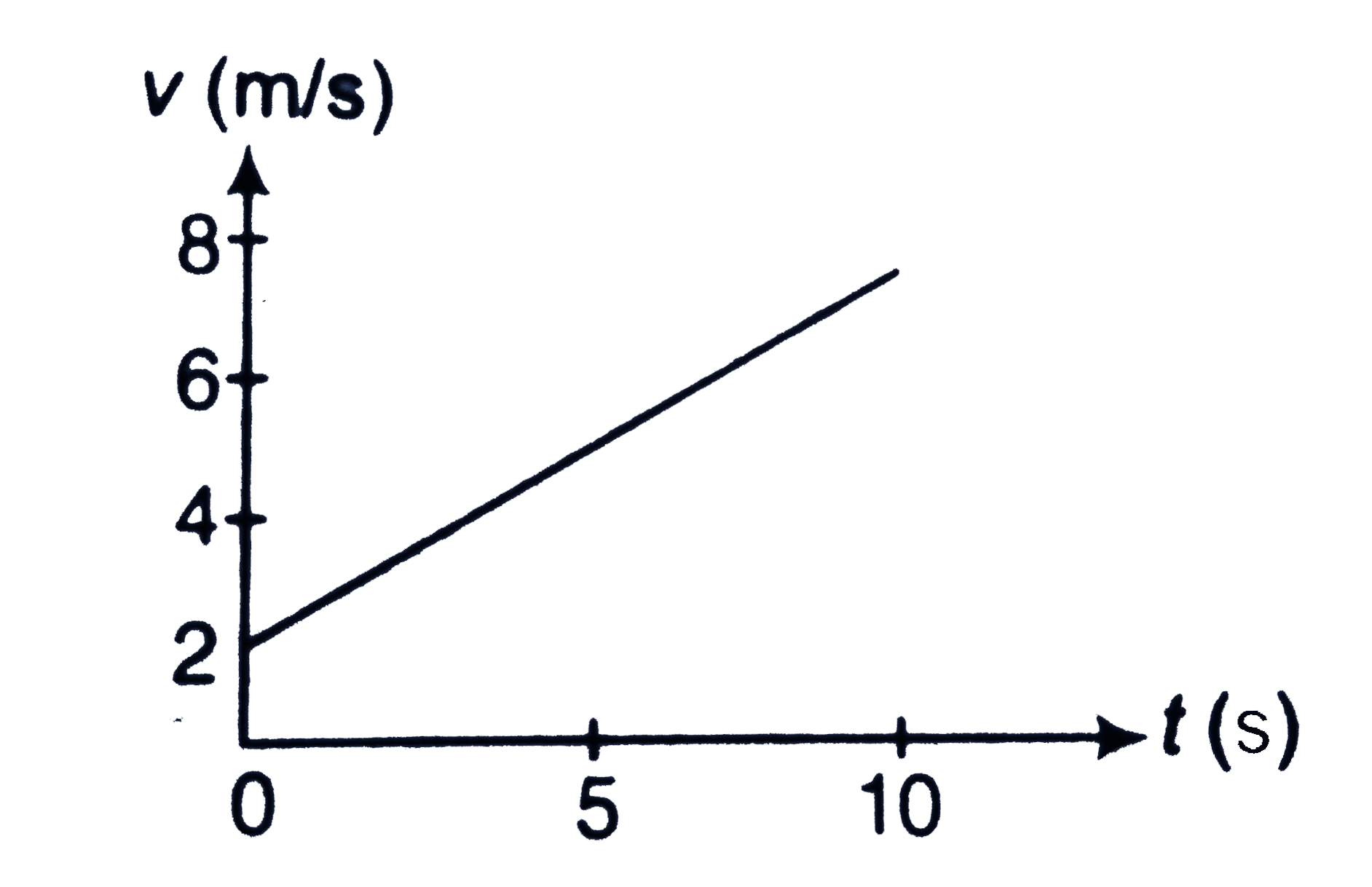
 shows the graph of velocity versus tie for a particle going along the X-axis. Find a. the acceleration, b. The distance travelled in 0 to 10 s and c. the displacement in 0 to 10 s.
shows the graph of velocity versus tie for a particle going along the X-axis. Find a. the acceleration, b. The distance travelled in 0 to 10 s and c. the displacement in 0 to 10 s.
View SolutionFig. shows the graph of velocity versus time for a particle going along the x-axis. Find (a) acceleration, (b) the distance traveled in 0→10s and (c) the displacement in 0 to 10s.
View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
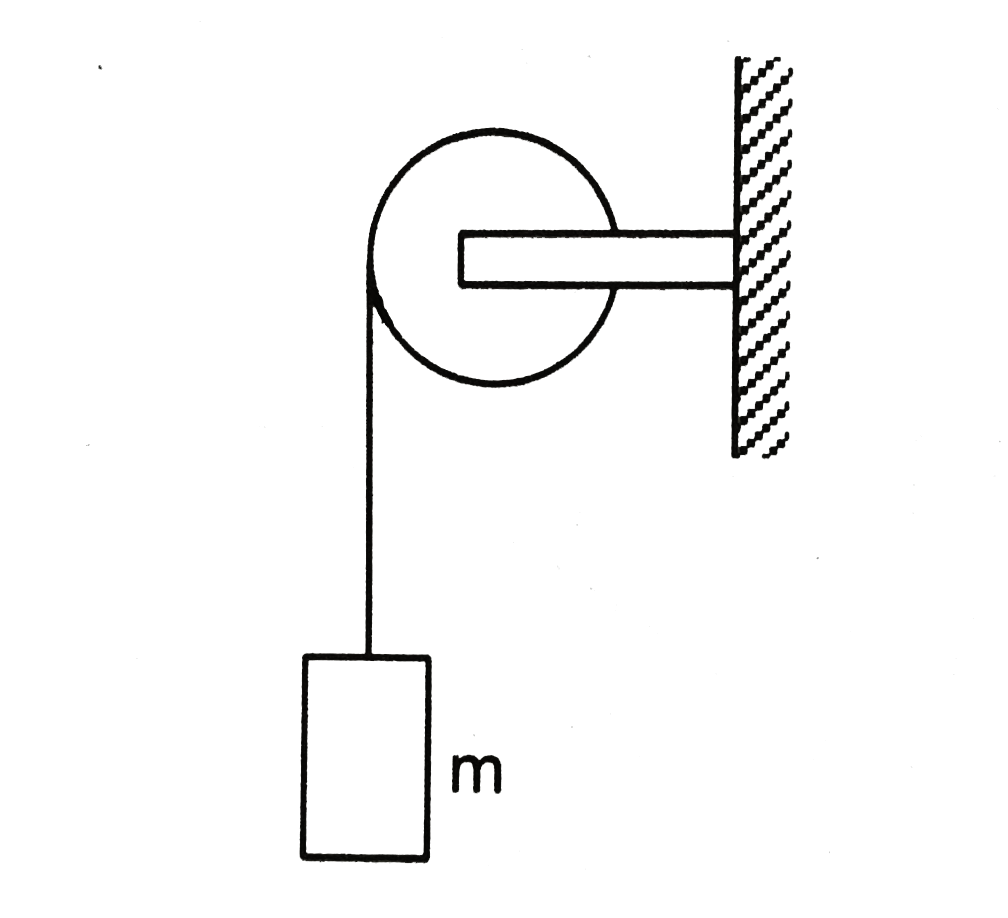
View SolutionA 4kg block is attached to a vertical rod by means of two strings of equal length. When the system rotates about the axis of the rod, the strings are extended as shown in figure.
(a) How many revolutions per minute must the system make in order for the tension in the upper string to be 200N ?
(b) What is the tension in the lower string then ?

View SolutionA 4kg block is attached to a vertical rod by means of two strings of equal length. When the system rotates about the axis of the rod, the strings are extended as shown in figure.
(a) How many revolutions per minute must the system make in order for the tension in the upper string to be 200N ?
(b) What is the tension in the lower string then ?

View SolutionFigure shows a solid uniform cylinder of radius R and mass M, which is free to rotate about a fixed horizontal axis O and passes through centre of the cylinder. One end of an ideal spring of force constant k is fixed and the other end is higed to the cylinder at A. Distance OA is equal to R2. An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass M and having cross sectional area A is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density ρ.
If in equilibrium, spring is horizontal and line OA is vertical, calculate frequency of small oscillations of the system.

View SolutionA wheel A is connected to a second wheel B by means of in extensible string, passing over a pulley C, which rotates about a fixed horizontal axle O, as shown in the figure. The system is released from rest. The wheel A rolls down the inclined plane OK thus pulling up wheel B which rolls along the inclined plane ON.
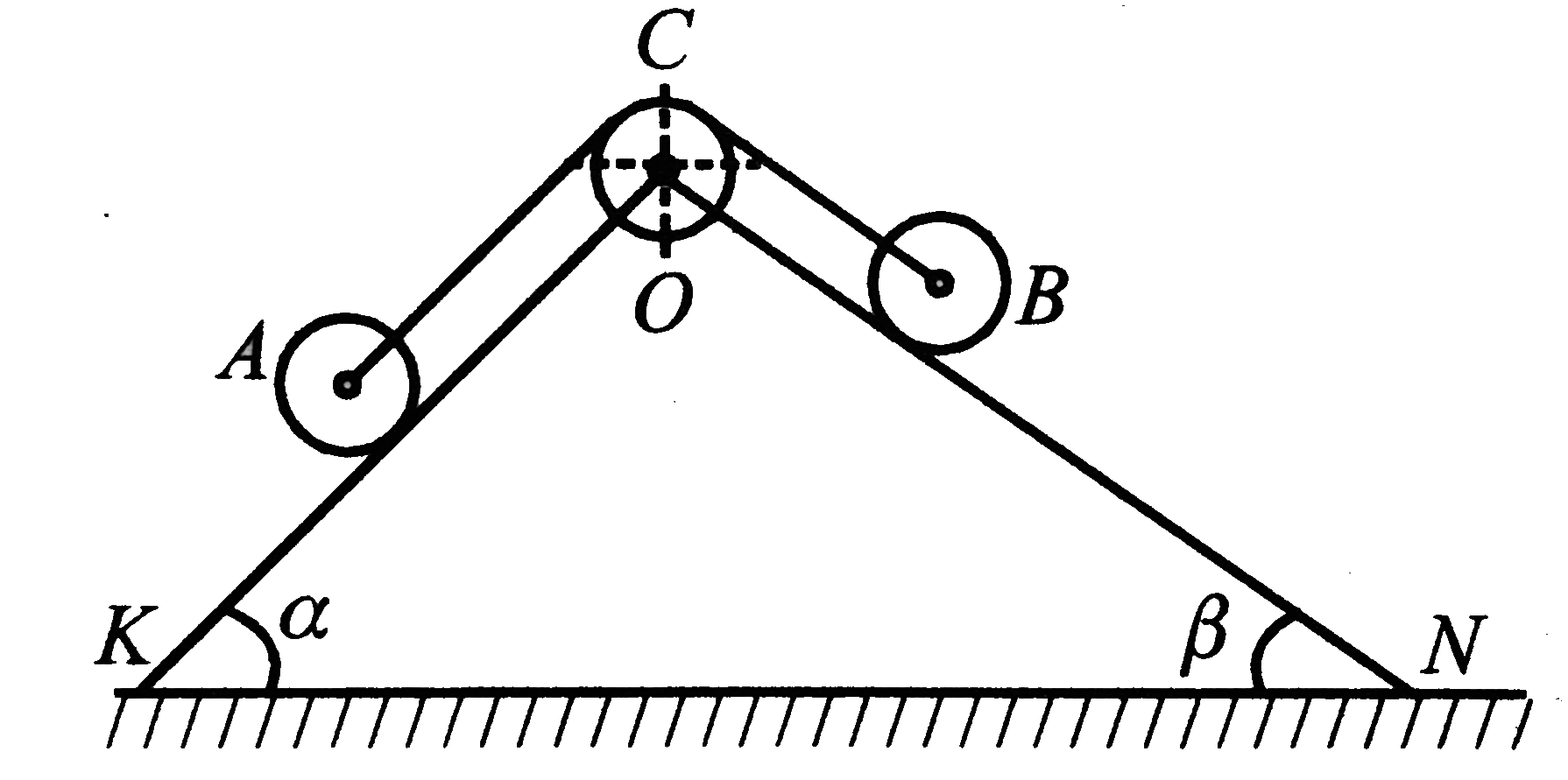
Determine the velocity (in m/s) of the axle of wheel A, when it has traveled a distance s=3.5m down the to be slope. Both wheels and the pulley are assumed homogeneous disks of identical weight and radius. Neglect the weight of the string. The string does not slip over C. [Take α=53∘ and β=37∘]
View Solution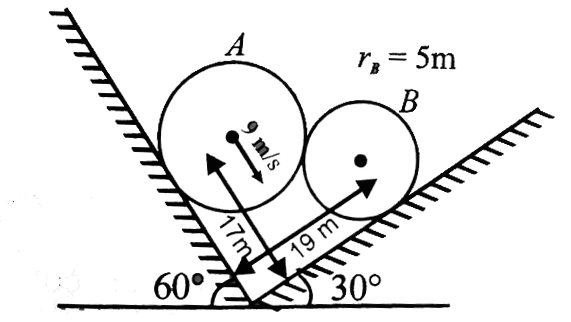
System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
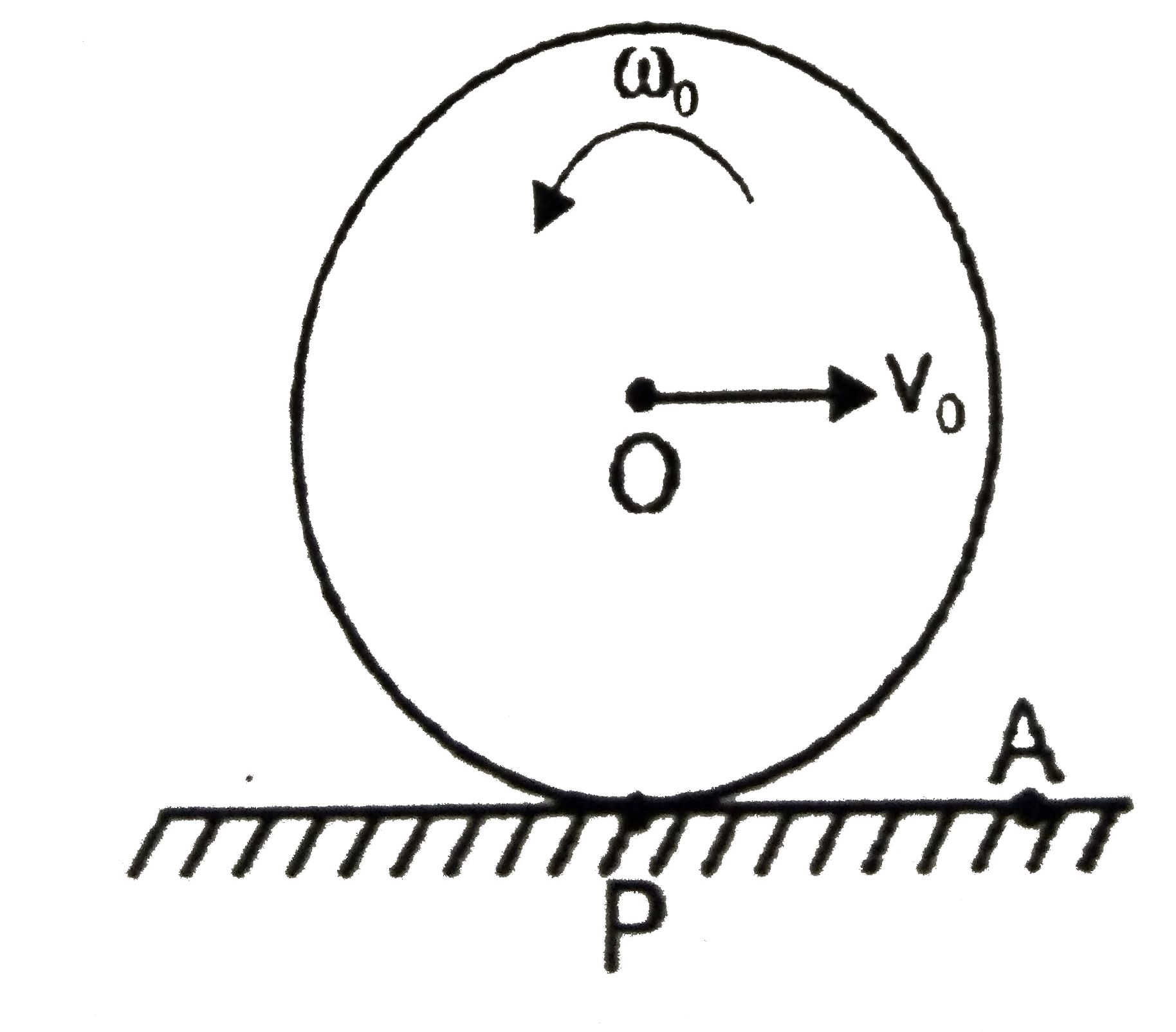
If above question , distance travelled by centre of mass of the wheel before it stops is −
View SolutionTwo discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -
View Solution
