Suppose →a is a vector of magnitude 4.5 unit due north. What is the vector 3→a
To solve the problem, we need to find the vector 3→a given that the vector →a has a magnitude of 4.5 units and is directed due north.
1. Identify the Original Vector:
- The vector →a has a magnitude of 4.5 units and is directed due north.
- We can represent this vector in terms of its components. Since it is directed north, we can write:
→a=4.5^j
where ^j is the unit vector in the north direction (positive y-direction).
2. Multiply the Vector by 3:
- To find the vector 3→a, we multiply the vector →a by 3:
3→a=3×(4.5^j)
3. Calculate the Magnitude:
- Performing the multiplication gives:
3→a=13.5^j
- This means the magnitude of the vector 3→a is 13.5 units.
4. Determine the Direction:
- Since we multiplied by a positive scalar (3), the direction of the vector remains the same as that of →a, which is due north.
5. Final Result:
- Therefore, the vector 3→a is:
3→a=13.5^j
- In terms of magnitude and direction, we can state:
- Magnitude: 13.5 units
- Direction: Due north
Summary:
The vector 3→a has a magnitude of 13.5 units and is directed due north.
---
- The vector →a has a magnitude of 4.5 units and is directed due north.
- We can represent this vector in terms of its components. Since it is directed north, we can write:
→a=4.5^j
where ^j is the unit vector in the north direction (positive y-direction).
- To find the vector 3→a, we multiply the vector →a by 3:
3→a=3×(4.5^j)
- Performing the multiplication gives:
3→a=13.5^j
- This means the magnitude of the vector 3→a is 13.5 units.
- Since we multiplied by a positive scalar (3), the direction of the vector remains the same as that of →a, which is due north.
- Therefore, the vector 3→a is:
3→a=13.5^j
- In terms of magnitude and direction, we can state:
- Magnitude: 13.5 units
- Direction: Due north
The vector 3→a has a magnitude of 13.5 units and is directed due north.
Similar Questions
Suppose →a is a vector of magnitude 4.5 unit due north. What is the vector a. 3→a,b−4→a?
View SolutionSuppose →a is a vector of magnitude 4.5 unit due north. What is the vector (a) 3→a (b) −4→a?
View SolutionSuppose →a is a vector of magnitude 4.5 unit due north. What is the vector −4→a?
View Solution→A is a vector of magnitude 2.7 units due east . What is the magnitude and direction of vector 4 →A ?
View SolutionFind a vector of magnitude 5 units, and parallel to the resultant of the vectors
→a=2ˆi+3ˆj−ˆkand→b=ˆi−2ˆj+ˆk.
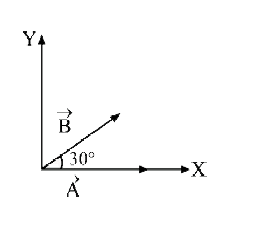
View SolutionVector →A of magnitude 4 units is directed along the positive x-axis. Another vector →B of magnitude 3 units lies in the x-y plane and is directed along 30∘ with the positive x-axis is as shown in figure. The magnitude of dot product →A.→B is:
View SolutionFind a vector of magnitude 9 units and perpendicular to the vectors
→a=4ˆi−ˆj+ˆkand→b=−2ˆi+ˆj−2ˆk.
View SolutionFind a vector whose magnitude is 3 units and which is perpendicular to the vectors →aand→b where →a=3ˆi+ˆj−4ˆkand→b=6ˆi+ˆj−2ˆk
View SolutionIf →a,→band→c are three vectors of which every pair is non colinear. If the vector →a+→band→b+→c are collinear with the vector →c and →a respectively then which one of the following is correct? (A) →a+→b+→c is a nul vector (B) →a+→b+→c is a unit vector (C) →a+→b+→c is a vector of magnitude 2 units (D) →a+→b+→c is a vector of magnitude 3 units
View SolutionThe vectors →A has a magnitude of 5 unit →B has a magnitude of 6 unit and the cross product of →Aand→B has a magnitude of 15 unit. Find the angle between →Aand→B.
View Solution
