ABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
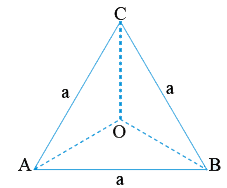
−−→AB+−−→BC+−−→CA
The correct Answer is:→0
−−→OA,−−→OBand−−→OC are three vectors of equal magnitude and are separated by 120∘ each ∴−−→OA+−−→OB+−−→OC=→0
Similar Questions
ABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
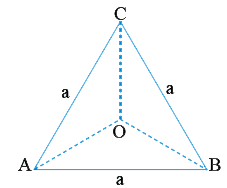
If ∣∣∣−−→AB+−−→BC+−−→AC∣∣∣=na then n = ?
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
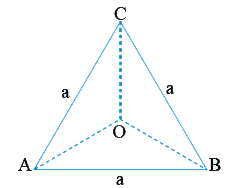
If −−→AB+−−→AC=n−−→AO then n = ?
View SolutionABC is an equilateral triangle of side 2m. If →E=10NC−1 then VA−VB is

View SolutionIf →a, →b, →c are the position vectors of the vertices of an equilateral triangle whose orthocentre is the origin, then write the value of →a+→b+→c
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View SolutionAssertion: If I is the incentre of △ABC,then|vec(BC)| vec(IA) +|vec(CA)| vec(IB) +|vec(AB)| vec(IC) =0Reason:IfOistheorig∈,thentheposition→−−→rofcentrof/_\ABCis−−→OA+−−→OB+−−→OC3
View SolutionABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View SolutionIf ABCD is a quadrilateral, then −−→BA+−−→BC+−−→CD+−−→DA=
View SolutionGiven an equilateral triangle ABC with side length equal to 'a'. Let M and N be two points respectivelyАВIn the side AB and AC such that −−→AN=K−−→ACand−−→AM=−−→AB3 If −−→BNand−−→CM are orthogonalthen the value of K is equal to
View SolutionIf G is the centroid of ΔABCandG' is the centroid of ΔA'B'C' then −−→AA'+−−→BB'+−−→CC'=
View Solution
