Find the differentiation of the following:
(8)
The correct Answer is:0
To find the differentiation of the constant value 8, we will follow these steps:
Step 1: Define the function
Let y=8. Here, y is defined as a constant value.
Step 2: Set up the differentiation
We need to find the derivative of y with respect to x, which is denoted as dydx.
Step 3: Apply the differentiation rule for constants
According to the rules of differentiation, the derivative of a constant is always zero. Therefore, we can write:
dydx=ddx(8)=0
Step 4: State the final answer
Thus, the differentiation of the constant 8 is:
dydx=0
Summary
The differentiation of the constant 8 is 0.
---
Let y=8. Here, y is defined as a constant value.
We need to find the derivative of y with respect to x, which is denoted as dydx.
According to the rules of differentiation, the derivative of a constant is always zero. Therefore, we can write:
dydx=ddx(8)=0
Thus, the differentiation of the constant 8 is:
dydx=0
The differentiation of the constant 8 is 0.
Similar Questions
Find the differentiation of the following:
(−12)
View SolutionFind the differentiation of the following:
(√3)
View SolutionDifferentiate the following w.r.t x
16x8
View SolutionDifferentiate the following w.r.t.x
View SolutionDifferentiate the following w.r.t. x:
ex3
View SolutionDifferentiate the following function tan2x
View SolutionDifferentiate between the following:
(i) Efflorescence and Deliquescence
View SolutionDifferentiate between the following acids :
(a)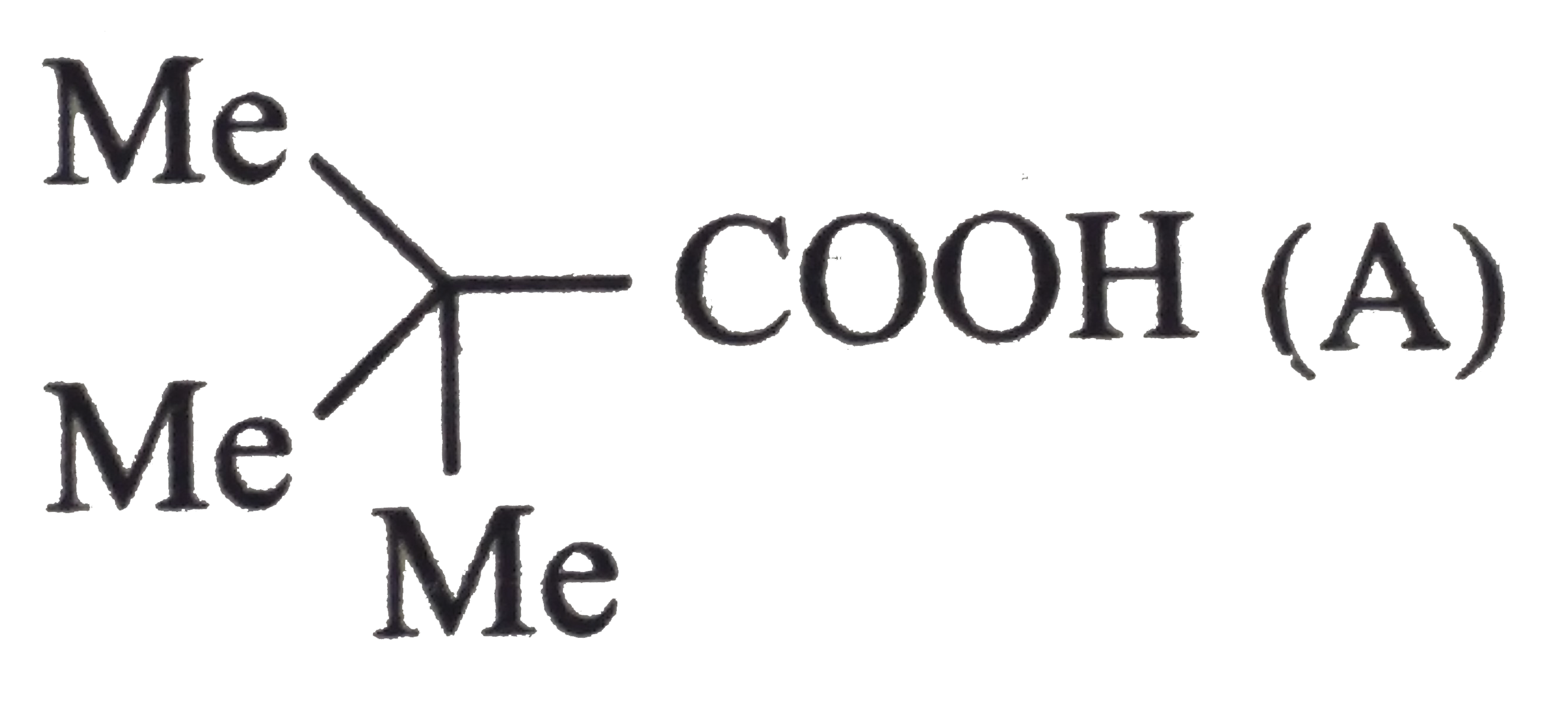
(b)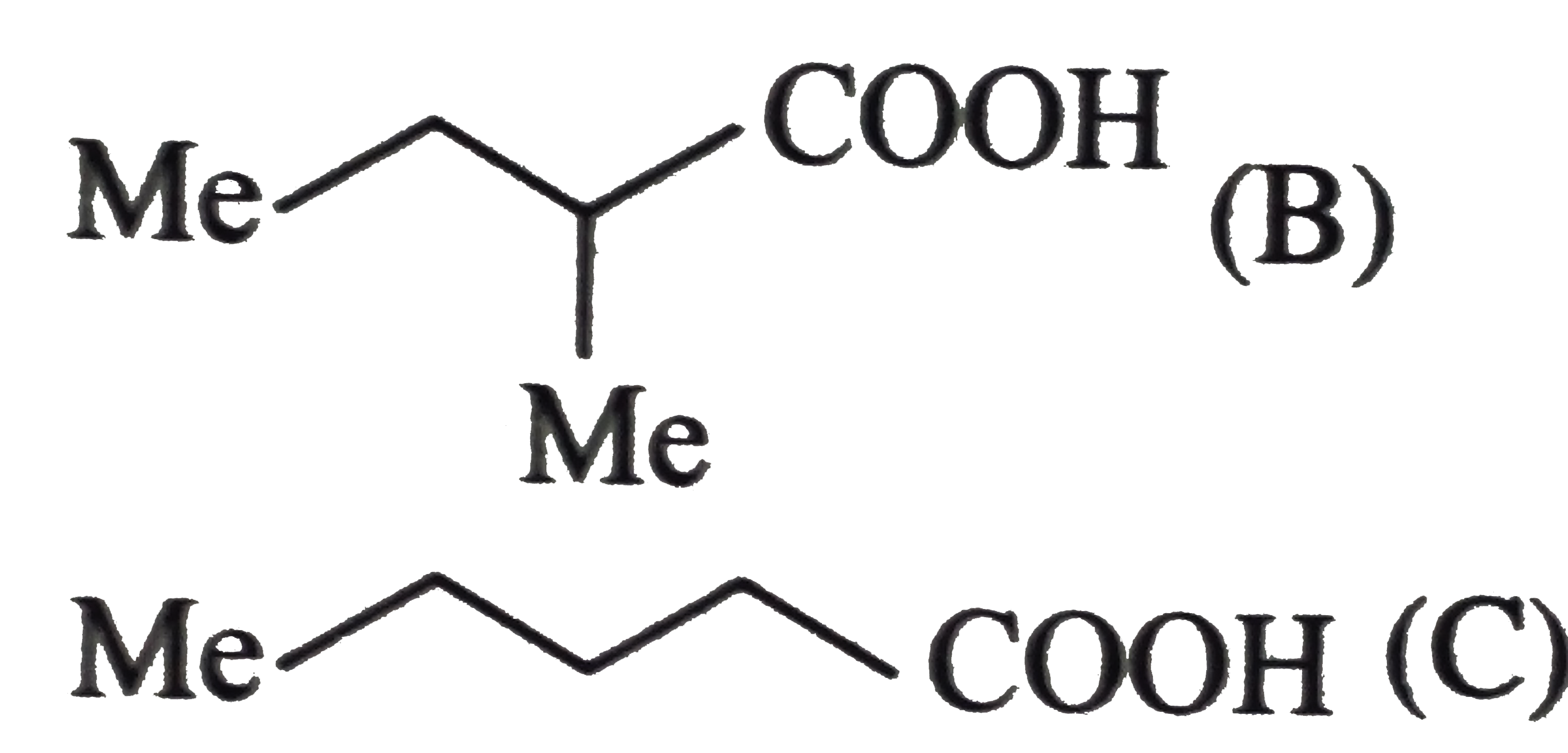
View SolutionDifferentiate each of the following from first principle: cos(x−π8)
View SolutionDifferentiate the following :
(ii) cos2xsinx
View Solution