The standard emf of a galvanic cell involving 2 motes of electrons in its redox reaction is 0.59 V the equilibriun constant for the redox reaction of the cell is
1020
105
10
1010
The correct Answer is:A
To solve the problem of finding the equilibrium constant (K_eq) for a redox reaction in a galvanic cell with a standard EMF (E°) of 0.59 V and involving 2 moles of electrons, we can use the Nernst equation in its equilibrium form.
1. Understand the relationship between E° and K_eq:
The relationship between the standard EMF of the cell (E°) and the equilibrium constant (K_eq) is given by the equation:
E°=0.0591nlogKeq
where:
- E° is the standard EMF of the cell,
- n is the number of moles of electrons transferred in the redox reaction,
- K_eq is the equilibrium constant.
2. Substitute the known values:
From the problem, we know:
- E° = 0.59 V
- n = 2 moles of electrons
Plugging these values into the equation gives:
0.59=0.05912logKeq
3. Rearrange the equation to solve for log K_eq:
Multiply both sides of the equation by 2:
2×0.59=0.0591logKeq
1.18=0.0591logKeq
4. Divide both sides by 0.0591:
logKeq=1.180.0591
Calculate the right side:
logKeq≈19.97
5. Convert log K_eq to K_eq:
To find K_eq, we take the antilog (base 10) of both sides:
Keq=1019.97
6. Approximate K_eq:
Since 1019.97≈1020, we conclude:
Keq≈1020
Final Answer:
The equilibrium constant (K_eq) for the redox reaction of the cell is approximately 1020.
---
The relationship between the standard EMF of the cell (E°) and the equilibrium constant (K_eq) is given by the equation:
E°=0.0591nlogKeq
where:
- E° is the standard EMF of the cell,
- n is the number of moles of electrons transferred in the redox reaction,
- K_eq is the equilibrium constant.
From the problem, we know:
- E° = 0.59 V
- n = 2 moles of electrons
0.59=0.05912logKeq
Multiply both sides of the equation by 2:
2×0.59=0.0591logKeq
1.18=0.0591logKeq
logKeq=1.180.0591
Calculate the right side:
logKeq≈19.97
To find K_eq, we take the antilog (base 10) of both sides:
Keq=1019.97
Since 1019.97≈1020, we conclude:
Keq≈1020
The equilibrium constant (K_eq) for the redox reaction of the cell is approximately 1020.
Topper's Solved these Questions
- ELECTROCHEMISTRYBook:VMC MODULES ENGLISHChapter:ELECTROCHEMISTRYExercise:Level-2
Explore 65 Videos
- ELECTROCHEMISTRYBook:VMC MODULES ENGLISHChapter:ELECTROCHEMISTRYExercise:JEE Main (Archive)
Explore 57 Videos
- ELECTROCHEMISTRYBook:VMC MODULES ENGLISHChapter:ELECTROCHEMISTRYExercise:Level-0 (Long Answer Type ) (5 Marks)
Explore 1 Video
- CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES Book:VMC MODULES ENGLISHChapter:CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES Exercise:JEE ADVANCE (ARCHIVE)
Explore 30 Videos
- ENVIRONMENTAL CHEMISTRYBook:VMC MODULES ENGLISHChapter:ENVIRONMENTAL CHEMISTRYExercise:JEE Main (Archive)
Explore 39 Videos
Similar Questions
The standard emf of a galvanic cell involving cell reaction with n=2 is found to be 0.295V at 25∘C. The equilibrium constant of the reaction would be (GivenF=96,500Cmol−1,R=8.314JK−1mol−1):
View SolutionAt 25∘C, the standard emf of a cell having reaction involving two electrons change is found to be 0.295 V. The equilibrium constant of the reaction is :
View SolutionThe standard e.m.f of a cell, involving one electron change is found to be 0.591 V at 25∘C. The equilibrium constant of the reaction is : (F=96,500Cmol−1: R=8.314 Jk−1mol−1
View SolutionA redox reaction always involves
View SolutionThe emf of a galvanic cell is positive when free energy change of reaction is
View SolutionWhich of the following involves redox reaction?
View SolutionThe standard potential of a cell using the reaction
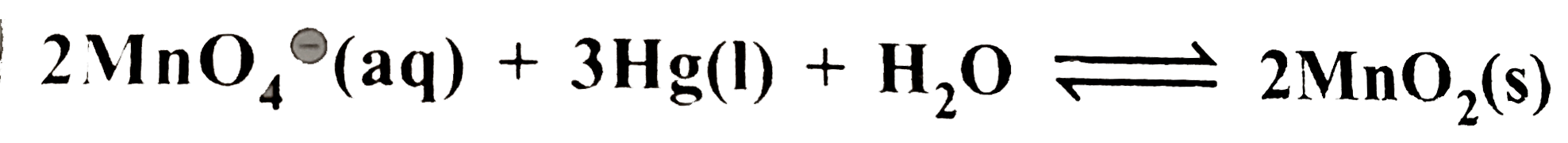 +3HgO(s)+2(c−OH)(aq) is 0.489V at 25∘C. What is the equilibrium constant of the reaction ?
+3HgO(s)+2(c−OH)(aq) is 0.489V at 25∘C. What is the equilibrium constant of the reaction ?
View SolutionFor the feasibility of a redox reaction in a cell, the emf should be.
View SolutionFor a cell involving one electron E0cell=0.59V and 298K, the equilibrium constant for the cell reaction is:
[Given that 2.303RTF=0.059V at T=298K]
View SolutionDerive an expression relating standard e.m.f. of the cell with the equilibrium constant of the cell reaction.
View Solution