A uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?

(μ21+μ2g(1+μ22)R) in clockwise direction.
(μ21+μkg1μ22R) in anticlockwise direction
2μ2(1+μ2)g1μ2kR in clockwise direction
2μg(1+μk)g1μ2kR in anticlockwise direction.
The correct Answer is:C
N1μR+N2μR=12mR2α⇒mgμ1+μ2+mgμ21+μ2=mRα2⇒α=2gμ(1+μ)R(1+μ2)
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (General rigid body motion, Rolling)
Explore 10 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Angular Momentum, Collision)
Explore 20 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Rotatinal Kinematics, Moment of Inertia)
Explore 10 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v0 and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is μ.
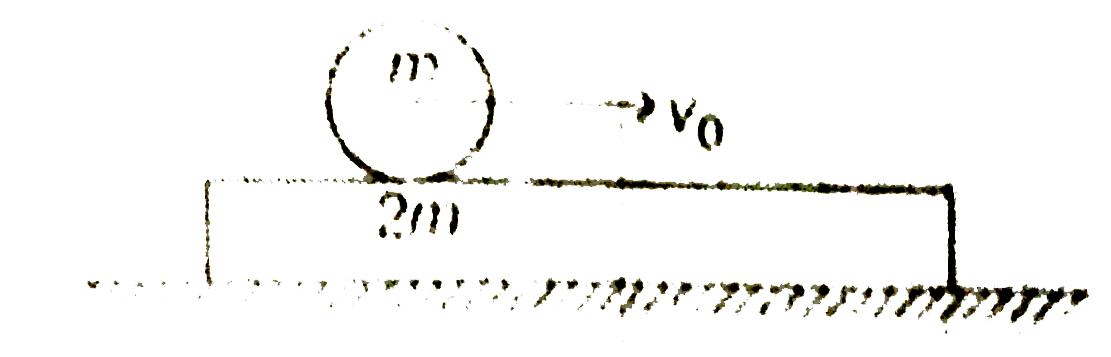
the cylinder given impluse t=0, than at what time pure rolling starts
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then

Option1
for pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is M a / 3
Option2
the maximum value of a, so that cyliner performs pure rolling is 3 μ g
Option3
The acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a / 3
Option4
none of these
View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA disc of radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4 (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=256kμgω0R. Find the value of k.
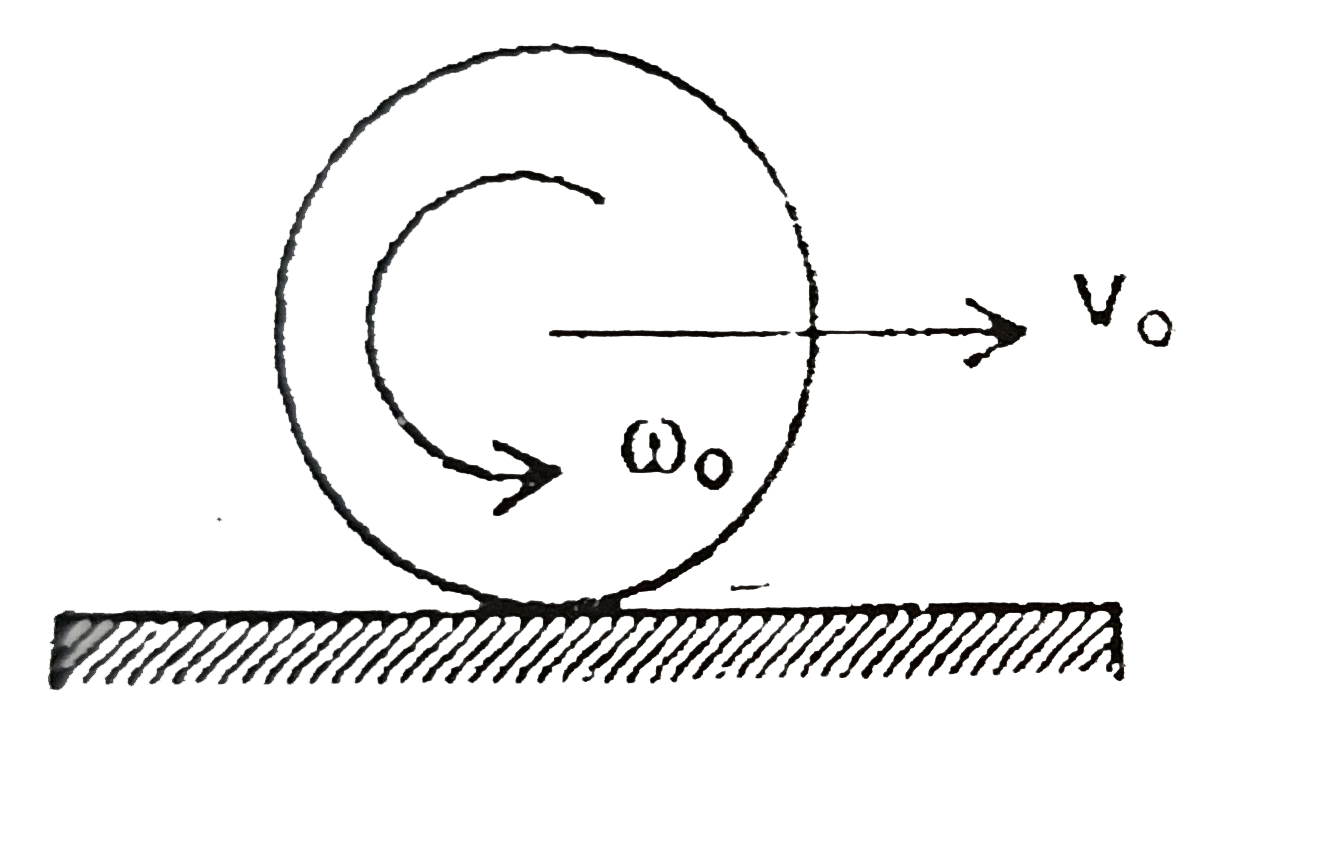
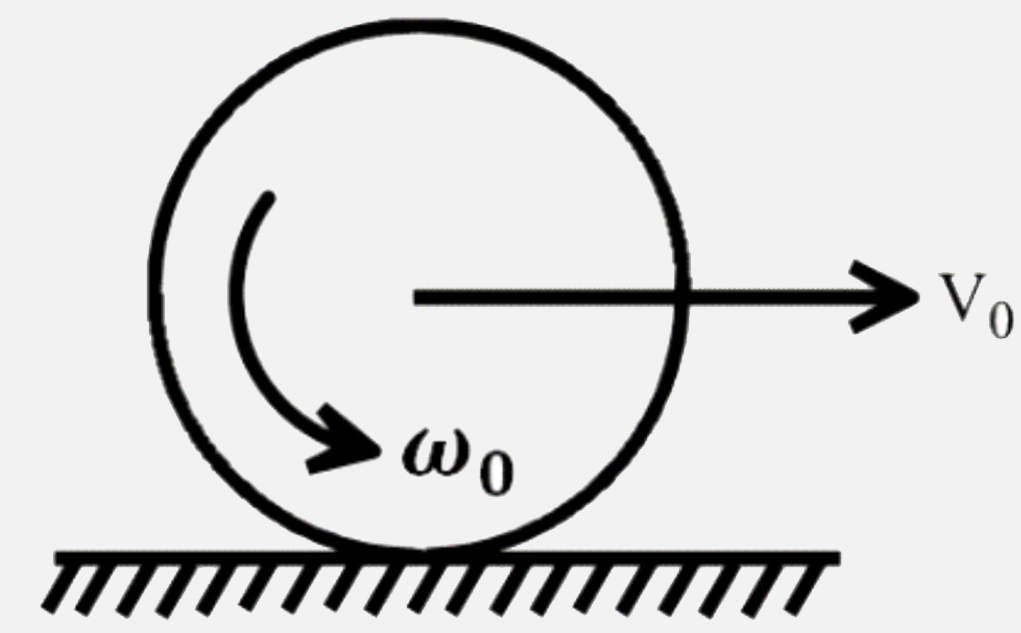
View SolutionA disc of the radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude (at t = 0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ . The sense of rotation and direction of its linear speed are shown in the figure . Choose the correct statement.
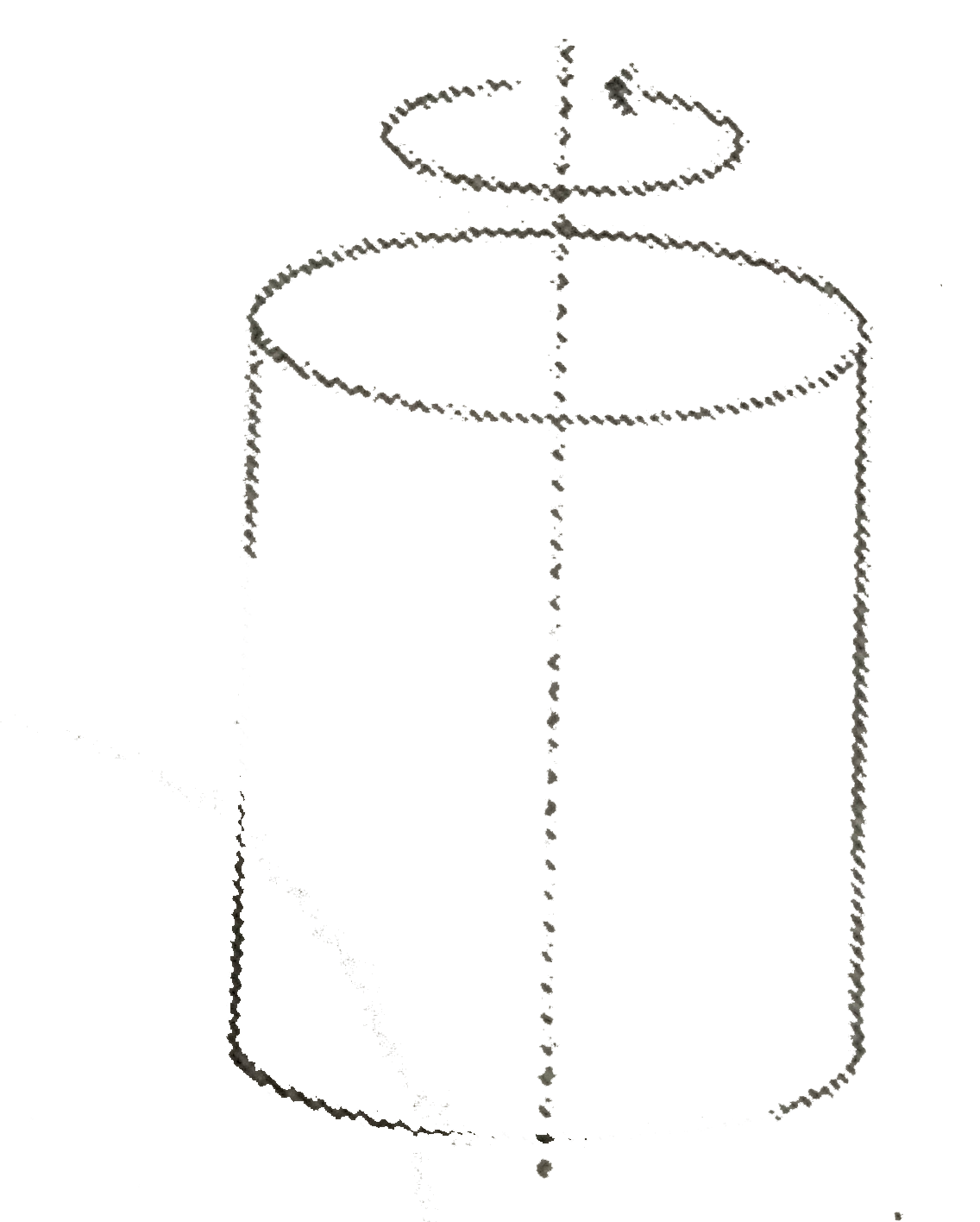
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
View SolutionA cylinder of water, is rotating about its own axis with uniform angular velocity ω. The shape of free surface of water will be
View Solution