A uniform disco of mass M and radius R, is resting on a table on its rim. The coeffecient of friction between disc and table is μ. Now the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?

(i) We know that moment of inertia, I=∑mr2 . In case of a hollow cylinder of radius R, all its mass (m) lies at a distance R from the axis of symmetry. But in case of solid sphere of radius R and mass M, most of its mass lies at a distance smaller than R. Hence, Icylinder>Isolid sphere (about the axes of symmetry)
(ii) If f is the force of friction acting on the disc and a is the acceleration produced in it due to applied force F, then
Ma= F-t............(i)
When the disc does not slide, a=Rα or α=aR
As Iα=Rf
(12MR2)(aR)=Rf or Ma = 2f............(ii)
From eqns.(i) and (ii), 2f=F-f or F=3f since there is no sliding, f≤μmg of F≤3μmg
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (LA: Long Answer Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1
45 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (SA-I: Short Answer Type-I)
7 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
Knowledge Check
A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is pulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?

 AμMgB2μMgC3μMgD4μMg
AμMgB2μMgC3μMgD4μMg
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
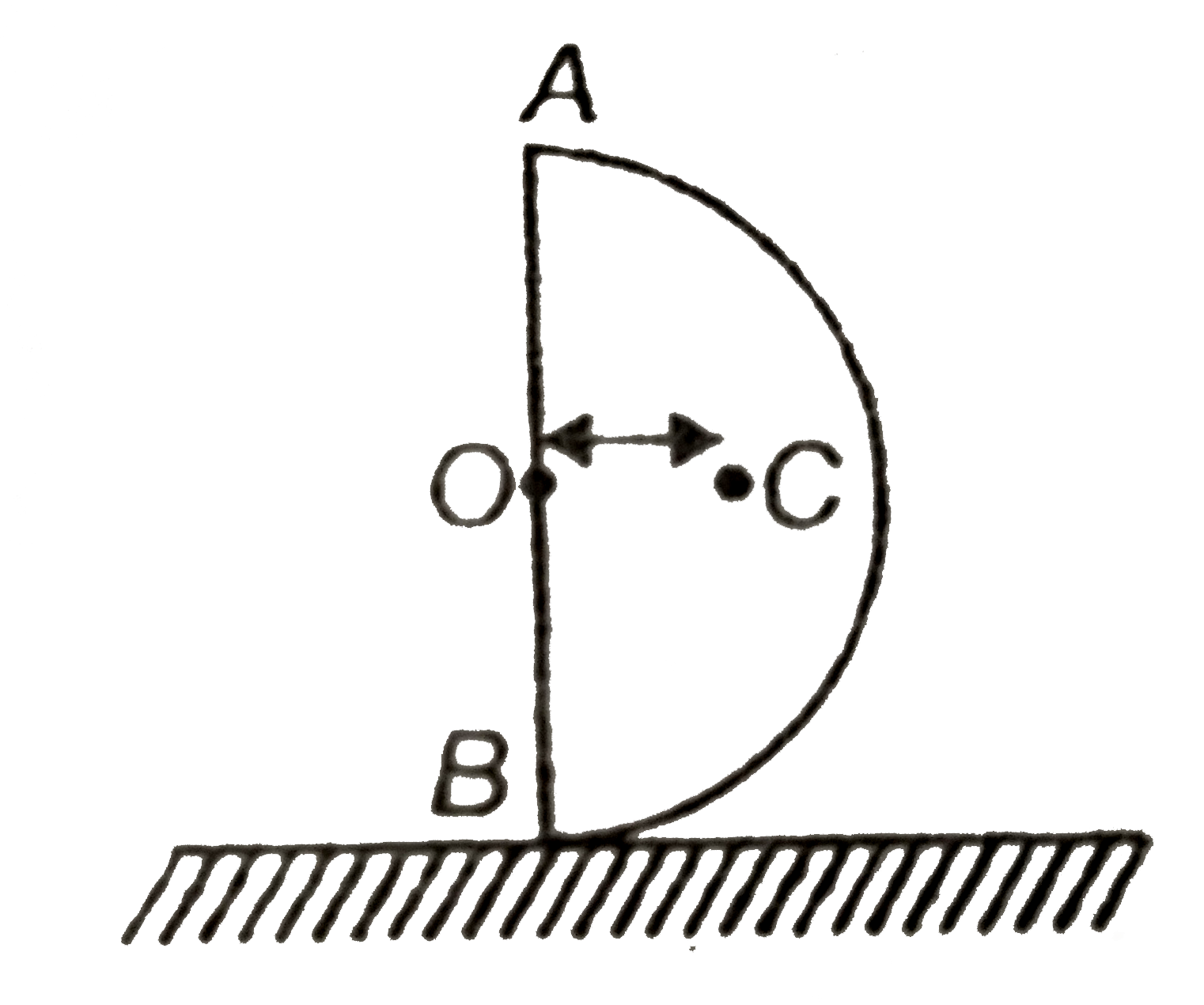
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View Solution
