A heater is designed to operate with a power of 1000 W in a 100 V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100 V mains as shown in the figure. What will be the value of R so that the heater operates with a power of 62.5 W?
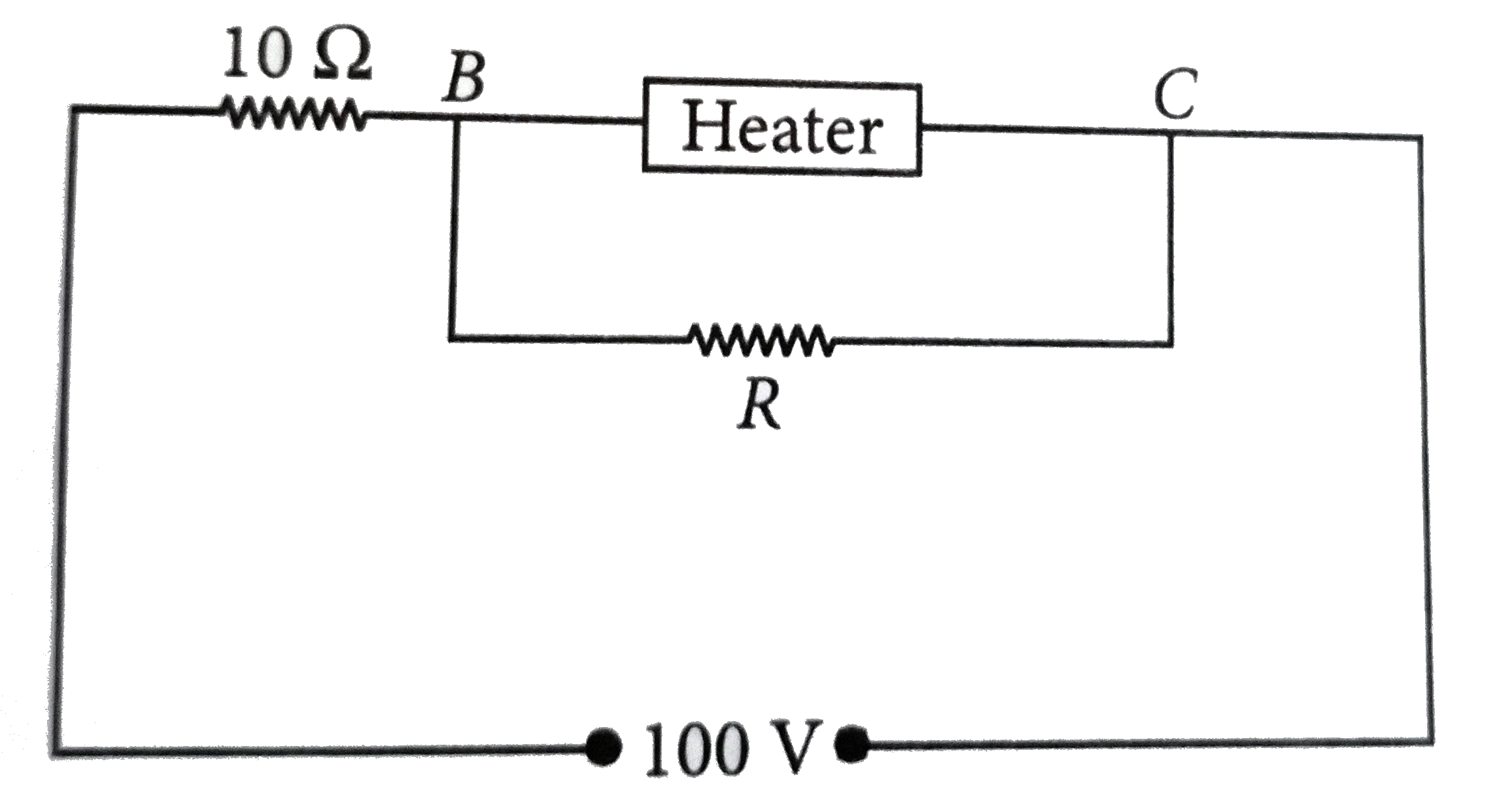
From P=V2R , Resistance of heater , R=V2P=(100)21000=10Ω
From P=I2R Current required across heater for power of 62.5W
i=√PR=√62.510=2.5A, Main current in the circuit
I=10010+10R10+R=100(10+R)100+20R=10(10+R)10+2R
This current will distribute in inverse ratio of resistance between heater and R.
i=(R10+R)Ior2.5=(R10+R)[(10(10+R))(10+2R)]=10R10+2R
SOlving this equation we get R=5Ω
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 JEE MAIN ARCHIVE
93 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
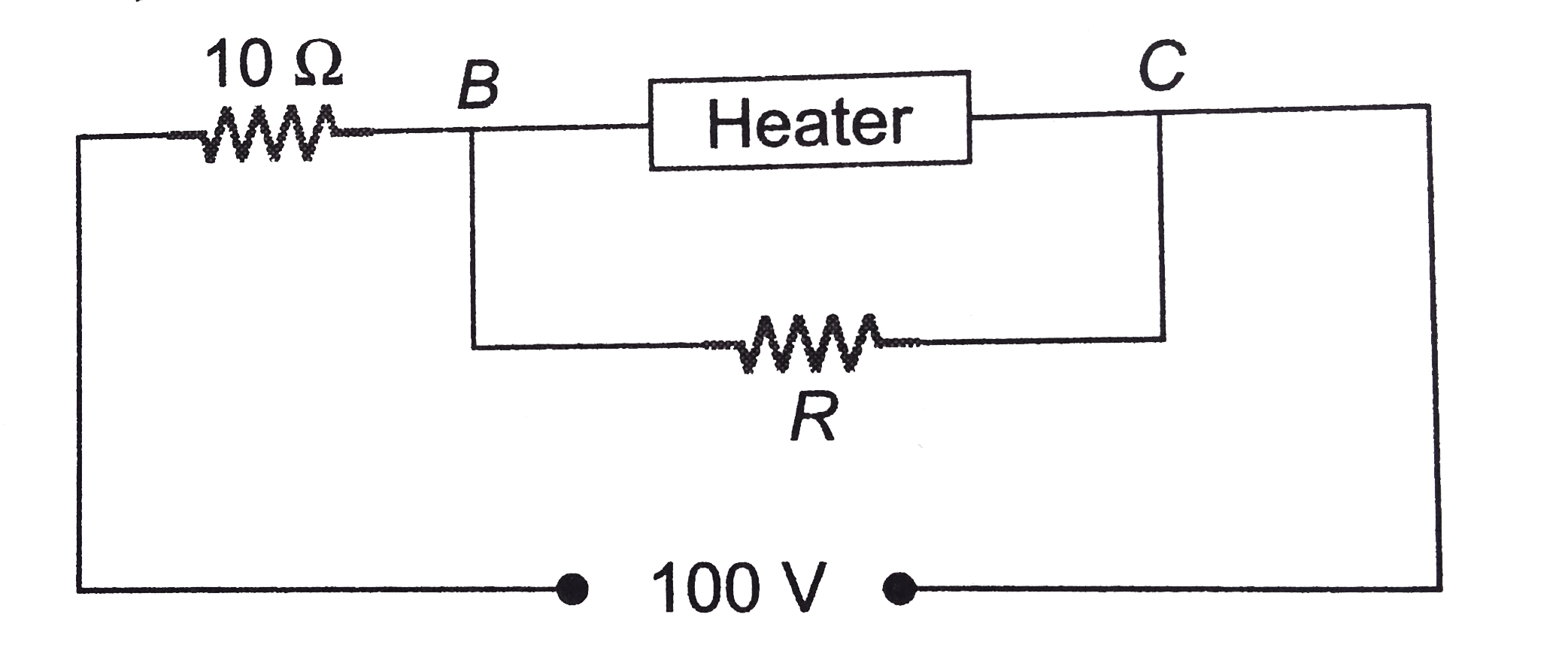
A heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100V mains as shown in figure. What will be the value of R so that the heater operates with a power of 62.5W?
View SolutionThe power dissipated in the circuit shown in the figure is 30 W. The value of R is
View Solution
Knowledge Check
A heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100V mains as shown in figure. What will be the value of R so that the heater operates with a power of 62.5W?
 A15ΩB10ΩC5ΩD25Ω
A15ΩB10ΩC5ΩD25Ω
Five identical lamps each of resistance R = 1500 Ω are connected to 300 V as shown in figure . The reading of ideal ammeter A is
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
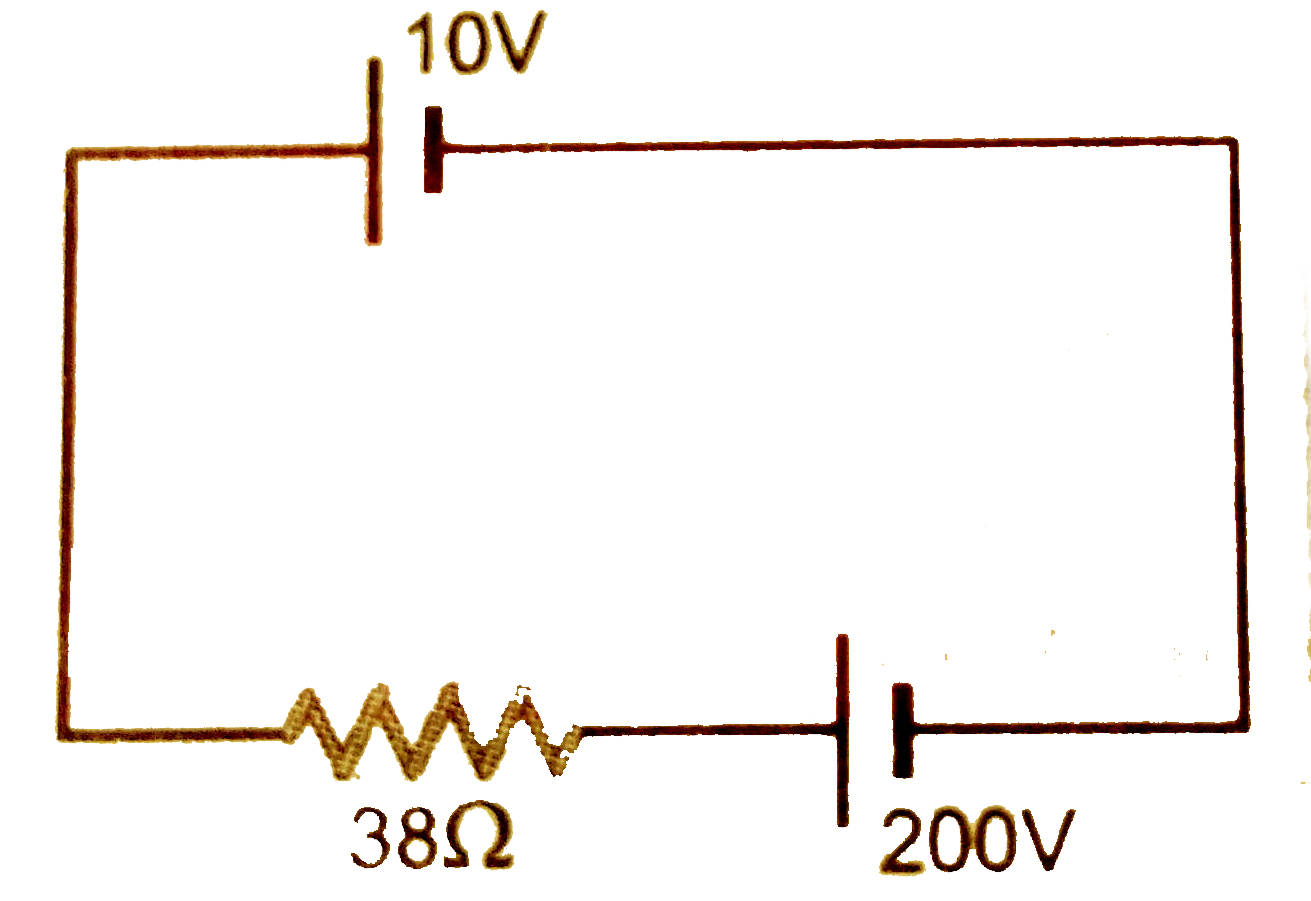 . Find the value of current in the circuit.
. Find the value of current in the circuit.
View SolutionA 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
View SolutionA 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor is
View SolutionThe resistance of a heater coil is 110Ω. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11Ω to a 220V main line. The heater operates with a power of 110W. The value of R in Ω is
View SolutionA 100W bulb designed to operate on 100V is to be connected across a 500V source . Find the resistance to be put in series so that bulb consumes 100W only.
View Solution

