Thermal decomposition of gaseous to gaseous at takes place according to the following equation:
The standard reaction Gibbs energy , of this reaction is positive. At the start of the reaction, there is one mole of and no . As the reaction proceeds, the number of moles of formed is given by . Thus is the number of moles of formed at equilibrium. The reaction is carried out at a constant total pressure of 2 bar. Consider the gases to behave ideally.
[Given, bar )
The equilibrium constant for this reaction at , in terms of is
The correct Answer is:b
To solve the problem step by step, we need to analyze the reaction and the conditions given.
Step 1: Write the reaction and initial conditions
The reaction is given as:
X2(g)⇌2X(g)
At the start of the reaction:
- Moles of X2=1
- Moles of X=0
Step 2: Define the change in moles
Let β be the number of moles of X formed at equilibrium. Therefore, at equilibrium:
- Moles of X2=1−β2 (since 1 mole of X2 produces 2 moles of X)
- Moles of X=β
Step 3: Calculate total moles at equilibrium
The total number of moles at equilibrium is:
ntotal=(1−β2)+β=1+β2
Step 4: Calculate mole fractions
The mole fraction of X and X2 can be calculated as follows:
- Mole fraction of X:
YX=βntotal=β1+β2
- Mole fraction of X2:
YX2=1−β2ntotal=1−β21+β2
Step 5: Calculate partial pressures
Using the total pressure P=2bar:
- Partial pressure of X:
PX=YX⋅P=β1+β2⋅2
- Partial pressure of X2:
PX2=YX2⋅P=1−β21+β2⋅2
Step 6: Write the expression for Kp
The equilibrium constant Kp for the reaction is given by:
Kp=(PX)2PX2
Substituting the expressions for PX and PX2:
Kp=(2β1+β2)22(1−β2)1+β2
Step 7: Simplify the expression
1. The numerator becomes:
⎛⎜⎝2β1+β2⎞⎟⎠2=4β2(1+β2)2
2. The denominator simplifies to:
2(1−β2)1+β2
Thus, we have:
Kp=4β2(1+β2)2⋅1+β22(1−β2)
3. Simplifying further:
Kp=4β22(1−β2)⋅(1+β2)=2β2(1−β2)(1+β2)
4. Recognizing that (1−β2)(1+β2)=1−(β2)2=1−β24, we can write:
Kp=2β21−β24
Final Expression for Kp
Thus, the equilibrium constant Kp in terms of β is:
Kp=8β24−β2
The reaction is given as:
X2(g)⇌2X(g)
- Moles of X2=1
- Moles of X=0
Let β be the number of moles of X formed at equilibrium. Therefore, at equilibrium:
- Moles of X2=1−β2 (since 1 mole of X2 produces 2 moles of X)
- Moles of X=β
The total number of moles at equilibrium is:
ntotal=(1−β2)+β=1+β2
The mole fraction of X and X2 can be calculated as follows:
- Mole fraction of X:
YX=βntotal=β1+β2
YX2=1−β2ntotal=1−β21+β2
Using the total pressure P=2bar:
- Partial pressure of X:
PX=YX⋅P=β1+β2⋅2
PX2=YX2⋅P=1−β21+β2⋅2
The equilibrium constant Kp for the reaction is given by:
Kp=(PX)2PX2
Kp=(2β1+β2)22(1−β2)1+β2
1. The numerator becomes:
⎛⎜⎝2β1+β2⎞⎟⎠2=4β2(1+β2)2
2(1−β2)1+β2
Kp=4β2(1+β2)2⋅1+β22(1−β2)
Kp=4β22(1−β2)⋅(1+β2)=2β2(1−β2)(1+β2)
Kp=2β21−β24
Thus, the equilibrium constant Kp in terms of β is:
Kp=8β24−β2
Topper's Solved these Questions
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:JEE (MAIN ARCHIVE)
Explore 32 Videos
- THERMOCHEMISTRYBook:VMC MODULES ENGLISHChapter:THERMOCHEMISTRYExercise:JEE ADVANCED (ARCHIVE)
Explore 31 Videos
- THERMODYNAMICS & THERMOCHEMISTRYBook:VMC MODULES ENGLISHChapter:THERMODYNAMICS & THERMOCHEMISTRYExercise:Impeccable
Explore 48 Videos
Similar Questions
The equilibrium constant for the reaction w+x⇔y+z is 9. If one mole of each of w and x are mixed and there is no change in volume, the number of moles of y for formed is
View Solution5 mole of X are mixed with 3 moles of Y. At equilibrium for the reaction, X+Y→Z 2 moles of Z are formed. The equilibrium constant for the reaction will be
View Solution
Knowledge Check
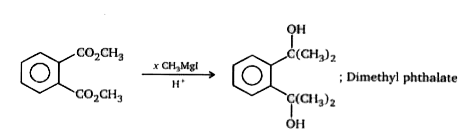
Number of moles (x) of Grignard reagent consumed in the above reaction is :A2B3C4D5
For the reaction, X+2Y→Z
5 moles of X and 9 moles of Y will produce:
View SolutionConsider the following spontaneous reaction 3X2(g)→2X3(g). What are the sign of ΔH, ΔS and ΔG for the reaction ?
View SolutionHydrogen (a moles ) and iodine (b moles ) react to give 2x moles of the HI at equilibrium . The total number of moles at equilibrium is
View SolutionFor the water gas reaction
C(s)+H2O(g)⇔CO(g)+H2(g)
The standard Gibb's energy of energy of reaction (at 1000K) is −8.1KJmol−1. Value of equilibrium constant is -
View SolutionWhen 1 mole of N2 and 1 mole of H2 is enclosed in 3L vessel and the reaction is allowed to attain equilibrium , it is found that at equilibrium there is 'x' mole of H2 . The number of moles of NH3 formed would be
View SolutionIf α is the fraction of HI dissociated at equilibrium in the reaction, 2HI(g)⇔H2(g)+I2(g) starting with the 2 moles of HI. Then the total number of moles of reactants and products at equilibrium are
View Solution3 moles of A and 4 moles of B are mixed together and allowed to come into equilibrium according to the following reaction.
3A(g)+4B(g)→2C(g)+3D(g)
When equilibrium is reached, there is 1 mole of C. The equilibrium constant of the reaction is
View Solution

