For a given gas, which of the following relationships is correct at a given temperature ?
urms>uav>ump
urms<uav<ump
urms>uav<ump
urms<uav>ump
The correct Answer is:A
To solve the question regarding the relationships between the root mean square speed (VRMS), average speed (Vaverage), and most probable speed (Vmps) of a gas at a given temperature, we will follow these steps:
Step 1: Understand the Definitions
- Most Probable Speed (Vmps): The speed at which the maximum number of molecules are moving. It is given by the formula:
Vmps=√2RTM
- Average Speed (Vaverage): The mean speed of all molecules in the gas. It is calculated using the formula:
Vaverage=√8RTπM
- Root Mean Square Speed (VRMS): The square root of the average of the squares of the speeds of the gas molecules. It is given by:
Vrms=√3RTM
Step 2: Compare the Speeds
From the formulas, we can derive the relationships:
- The value of Vrms is greater than Vaverage, which is greater than Vmps.
- In numerical terms:
- Vrms=√3⋅√RTM≈1.732⋅√RTM
- Vaverage=√8π⋅√RTM≈1.595⋅√RTM
- Vmps=√2⋅√RTM≈1.414⋅√RTM
Step 3: Establish the Correct Relationship
From the above comparisons, we can conclude:
Vrms>Vaverage>Vmps
Thus, the correct relationship at a given temperature for a gas is:
Vrms>Vaverage>Vmps
Conclusion
The correct answer to the question is that the root mean square speed is greater than the average speed, which is in turn greater than the most probable speed.
- Most Probable Speed (Vmps): The speed at which the maximum number of molecules are moving. It is given by the formula:
Vmps=√2RTM
- Average Speed (Vaverage): The mean speed of all molecules in the gas. It is calculated using the formula:
Vaverage=√8RTπM
- Root Mean Square Speed (VRMS): The square root of the average of the squares of the speeds of the gas molecules. It is given by:
Vrms=√3RTM
From the formulas, we can derive the relationships:
- The value of Vrms is greater than Vaverage, which is greater than Vmps.
- In numerical terms:
- Vrms=√3⋅√RTM≈1.732⋅√RTM
- Vaverage=√8π⋅√RTM≈1.595⋅√RTM
- Vmps=√2⋅√RTM≈1.414⋅√RTM
From the above comparisons, we can conclude:
Vrms>Vaverage>Vmps
Thus, the correct relationship at a given temperature for a gas is:
Vrms>Vaverage>Vmps
The correct answer to the question is that the root mean square speed is greater than the average speed, which is in turn greater than the most probable speed.
Topper's Solved these Questions
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Level-2
50 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Level-2 (NUMBERICAL VALUE TYPE FOR JEE MAIN
15 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - LEVEL -0 (Short Answer Type-II)
27 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IMPECCABLE
50 Videos
- STOICHIOMETRY - IBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - JEE Advanced (Archive)
31 Videos
Similar Questions
Knowledge Check
Which of the following relationships is not correct ?
AΔH=ΔU+ΔngRTBΔHsub=ΔHfusion+ΔHvapCΔH∘r=ΣH∘f(reactants)−Σ∘f(products)DΔH∘r=ΣB.E. of reactants −ΣB.E. of productsIn which of the following reactions the correct product is given?
A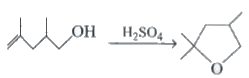 B
B C
C D
D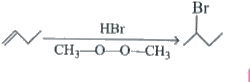
Which of the following options is correct for the given figures ?
 A X YHomogamyIsogamyB X YAnisogamyIsogamyC X YHeterogamyAnisogamyD X YIsogamyOogamy
A X YHomogamyIsogamyB X YAnisogamyIsogamyC X YHeterogamyAnisogamyD X YIsogamyOogamy
Which of the following option is correct for given curve?
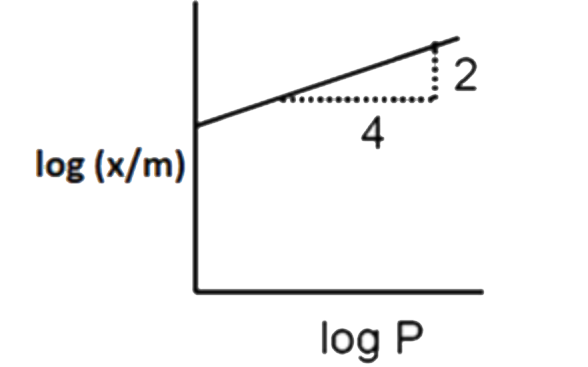
View SolutionFrom the given graph

Which of the following statement is correct ?
View SolutionWhich of the following gases has maximum rms speed at a given temperature?
View SolutionWhich of the following will increase with dilution at a given temperature?
View SolutionWhich of the following statements relationship is not correct?
View Solution

