The number of anti bonding electrons in N2 is
4
10
12
14
The correct Answer is:A
To determine the number of anti-bonding electrons in the nitrogen molecule (N₂), we can follow these steps:
Step 1: Determine the total number of electrons in N₂
Each nitrogen atom has an atomic number of 7, which means it has 7 electrons. Since there are two nitrogen atoms in N₂, the total number of electrons is:
Total electrons=7×2=14
Step 2: Write the molecular orbital configuration for N₂
The molecular orbital configuration for N₂ can be written by filling the molecular orbitals in order of increasing energy. The order of filling for N₂ is as follows:
- σ(1s)²
- σ*(1s)²
- σ(2s)²
- σ*(2s)²
- π(2p_x)² = π(2p_y)²
- σ(2p_z)²
So, the complete molecular orbital configuration for N₂ is:
σ(1s)2σ∗(1s)2σ(2s)2σ∗(2s)2π(2px)2π(2py)2σ(2pz)2
Step 3: Identify bonding and anti-bonding orbitals
In the configuration:
- Bonding orbitals: σ(1s), σ(2s), π(2p_x), π(2p_y), σ(2p_z)
- Anti-bonding orbitals: σ*(1s), σ*(2s)
Step 4: Count the number of electrons in the anti-bonding orbitals
From the configuration:
- σ*(1s) has 2 electrons
- σ*(2s) has 2 electrons
Adding these gives:
Total anti-bonding electrons=2+2=4
Conclusion
The number of anti-bonding electrons in N₂ is 4.
---
Each nitrogen atom has an atomic number of 7, which means it has 7 electrons. Since there are two nitrogen atoms in N₂, the total number of electrons is:
Total electrons=7×2=14
The molecular orbital configuration for N₂ can be written by filling the molecular orbitals in order of increasing energy. The order of filling for N₂ is as follows:
- σ(1s)²
- σ*(1s)²
- σ(2s)²
- σ*(2s)²
- π(2p_x)² = π(2p_y)²
- σ(2p_z)²
σ(1s)2σ∗(1s)2σ(2s)2σ∗(2s)2π(2px)2π(2py)2σ(2pz)2
In the configuration:
- Bonding orbitals: σ(1s), σ(2s), π(2p_x), π(2p_y), σ(2p_z)
- Anti-bonding orbitals: σ*(1s), σ*(2s)
From the configuration:
- σ*(1s) has 2 electrons
- σ*(2s) has 2 electrons
Total anti-bonding electrons=2+2=4
The number of anti-bonding electrons in N₂ is 4.
Topper's Solved these Questions
- CHEMICAL BONDING-I & IIBook:VMC MODULES ENGLISHChapter:CHEMICAL BONDING-I & IIExercise:Level - 2 (JEE Advanced)
Explore 50 Videos
- CHEMICAL BONDING-I & IIBook:VMC MODULES ENGLISHChapter:CHEMICAL BONDING-I & IIExercise:JEE Main (Numerical Value Questions)
Explore 15 Videos
- CHEMICAL BONDING-I & IIBook:VMC MODULES ENGLISHChapter:CHEMICAL BONDING-I & IIExercise:Level - 0 (Long Answer Type)
Explore 4 Videos
- CHEMICAL BONDING & MOLECULAR STRUCTURE Book:VMC MODULES ENGLISHChapter:CHEMICAL BONDING & MOLECULAR STRUCTURE Exercise:IN-CHAPTER EXERCISE-L
Explore 9 Videos
- CHEMICAL EQUILIBRIUMBook:VMC MODULES ENGLISHChapter:CHEMICAL EQUILIBRIUMExercise:IN-CHAPTER EXERCISE - G
Explore 10 Videos
Similar Questions
The number of non-bonding electrons of N2 is________.
View SolutionThe number of bonding electron pairs in N2 on the basis of molecular orbital theory is
View SolutionIf NB is the number of bonding electron and NA is the number of antibonding electrons of a molecules. Then choose the incorrect statement(s) for the relationship , NB>NA"
View SolutionIf NB is the number of bonding electron and NA is the number of antibonding electrons of a molecules. Then choose the incorrect statement(s) for the relationship , NB>NA"
View SolutionWhich of the following options represents the correct bond order?
Thinking process
To calcualte bond order, write the molecular orbital configuration of particular species and afterwards using the formula.
Bond order =12 [Number of bonding (N6) - Number of anti-bonding electrons (Na)]
View SolutionThe total number of lone pair of electrons in N2O3 is
View SolutionA sigma bonded molecule MX3 is T-shaped The number of non-bonding pairs of electrons is .
View SolutionThe total number of π-bond electrons in the following structure is
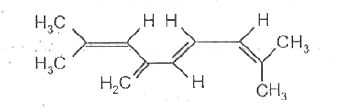
View SolutionIn phosphorus acid, if X is number of non bonding electron pairs. Y is number of σ-bonds and Z is number of π- bonds. Then, calculate value of Y×Z−X.
View SolutionIn phosphorus acid, if X is number of non bonding electron pairs. Y is number of σ-bonds and Z is number of π- bonds. Then, calculate value of Y×Z−X.
View Solution
