A parallel combination of 0.1 MΩ resistor and a 10μF capacitor is connected across a 1.5 V source of negligible resistance. The time (in sec) required for the capacitor to get charged upto 0.75 V is approximately
Infinite
loge2
log102
zero
The correct Answer is:D
To solve the problem, we need to determine the time required for a capacitor to charge up to a certain voltage when connected in parallel with a resistor across a voltage source.
1. Identify the Components:
We have a resistor (R) of 0.1 MΩ (which is 0.1 x 10^6 Ω = 100,000 Ω) and a capacitor (C) of 10 µF (which is 10 x 10^-6 F = 0.00001 F) connected in parallel across a 1.5 V source.
2. Understand the Charging Equation:
The voltage across a charging capacitor in a circuit can be described by the equation:
V(t)=V0(1−e−tRC)
where:
- V(t) is the voltage across the capacitor at time t,
- V0 is the final voltage (1.5 V in this case),
- R is the resistance,
- C is the capacitance,
- e is the base of the natural logarithm.
3. Calculate the Time Constant (τ):
The time constant τ is given by:
τ=RC
Substituting the values:
R=0.1×106Ω=100,000Ω
C=10×10−6F=0.00001F
Therefore:
τ=100,000×0.00001=1sec
4. Set Up the Equation for Charging to 0.75 V:
We want to find the time t when the voltage across the capacitor V(t) is 0.75 V:
0.75=1.5(1−e−t1)
Simplifying this:
0.75=1.5−1.5e−t
Rearranging gives:
1.5e−t=1.5−0.75=0.75
Dividing both sides by 1.5:
e−t=0.751.5=0.5
5. Solve for t:
Taking the natural logarithm of both sides:
−t=ln(0.5)
Therefore:
t=−ln(0.5)≈0.693sec
Final Answer:
The time required for the capacitor to charge up to 0.75 V is approximately 0.693 seconds.
We have a resistor (R) of 0.1 MΩ (which is 0.1 x 10^6 Ω = 100,000 Ω) and a capacitor (C) of 10 µF (which is 10 x 10^-6 F = 0.00001 F) connected in parallel across a 1.5 V source.
The voltage across a charging capacitor in a circuit can be described by the equation:
V(t)=V0(1−e−tRC)
where:
- V(t) is the voltage across the capacitor at time t,
- V0 is the final voltage (1.5 V in this case),
- R is the resistance,
- C is the capacitance,
- e is the base of the natural logarithm.
The time constant τ is given by:
τ=RC
Substituting the values:
R=0.1×106Ω=100,000Ω
C=10×10−6F=0.00001F
Therefore:
τ=100,000×0.00001=1sec
We want to find the time t when the voltage across the capacitor V(t) is 0.75 V:
0.75=1.5(1−e−t1)
Simplifying this:
0.75=1.5−1.5e−t
Rearranging gives:
1.5e−t=1.5−0.75=0.75
Dividing both sides by 1.5:
e−t=0.751.5=0.5
Taking the natural logarithm of both sides:
−t=ln(0.5)
Therefore:
t=−ln(0.5)≈0.693sec
The time required for the capacitor to charge up to 0.75 V is approximately 0.693 seconds.
Topper's Solved these Questions
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 6
Explore 1 Video
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 7
Explore 1 Video
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 4
Explore 1 Video
- BASIC MATHEMATICS & VECTORSBook:VMC MODULES ENGLISHChapter:BASIC MATHEMATICS & VECTORSExercise:Impeccable
Explore 50 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
Similar Questions
A parallel combination of 0.1MΩ resistor and a 10μF capacitor is connected across a 1.5V source of negligible resistance. The time required for the capacitor to get charged up to 0.75 V is approximately (in seconds).
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View Solution
Knowledge Check
A 0.2kΩ resistor and 15μF capacitor are connected in series to a 220 V, 50 Hz ac source. The impadance of the circuit is
A250ΩB268ΩC29.15ΩD291.5Ω
Effective capacitance of parallel combination of two capacitors C1andC2 is 10μF. When the capacitors are individually connected to a voltage source of 1V, the energy stored in the capacitor C2 is 4 times of C1. If these capacitors are connected in series, their effective capacitor will be: lt
View SolutionHow many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
View SolutionA resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View SolutionA 8 μ F capacitor is charged by a 400 V supply through 0.1 M Ω resistance. The time taken by the capacitor to develop a potential difference of 300V is : (Given log104=0.602)
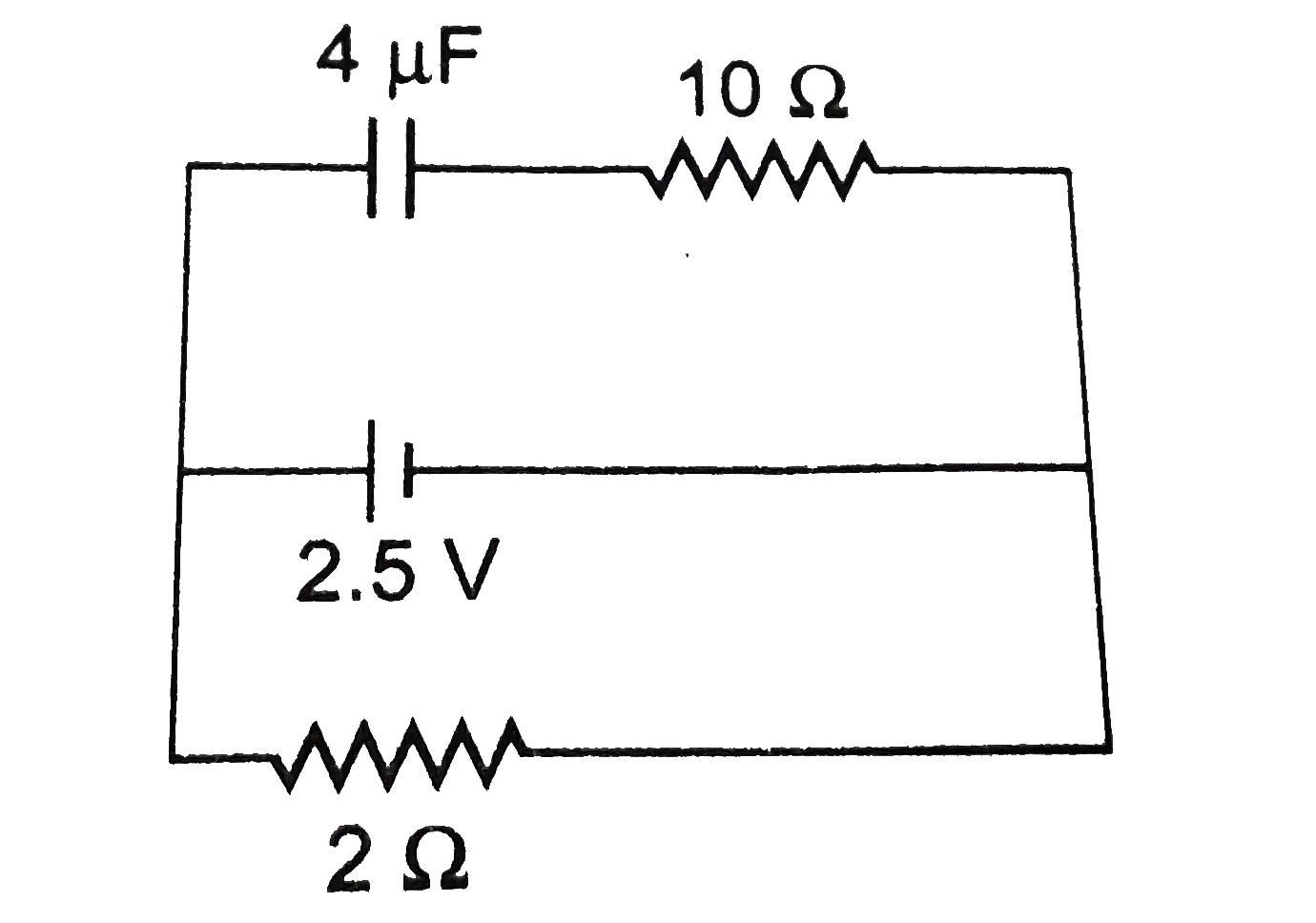
View SolutionA capacitor of 4μF is connected as shwon in the figure. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?

View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate :the current through each resistor
View Solution