Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is and L is its latent heat of vaporization.
The correct Answer is:D
If a layer of thickness dr is evaporated, then
Change in surface energy
= Change in surface area × T
As dr is very small , so neglected.
So change in surface energy
Energy required to evaporate layer of thickness
The processes of evaporation just starts, if change in surface energy is just sufficient to evaporate the water layer.
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced(Archive) Level - 2
Explore 1 Video
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2
Explore 29 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:Level -2
Explore 50 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:PHYSICS
Explore 30 Videos
Similar Questions
If the temperature of a liquid is increased, then its surface tension
View SolutionAssume that a rain drop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the rain drop.
View SolutionWhat should be the radius of a water drop so that the excess pressure inside it is 0.2 atm? Surface tension of water is 72×10−3N/m?
View SolutionOn heating a liquid, its surface tension
View SolutionIf a spherical rain drop evaporates at a rate proportional to its surface area. Form a differential equation indicating the rate of change of the radius of the rain drop.
View SolutionA spherical rain drop evaporates at a rate proportional to its surface area at any instant t. The differential equation giving the rate of change of the radius of the rain drop is _____
View SolutionA spherical rain drop evaporates at a rate proportional to its surface area at any instant t. The differential equation giving the rate of change of the radius of the rain drop is _____
View SolutionA liquid of diameter D breaks up into 64 tiny drops. If the surface tension of the liquid is σ what is the change in energy?
View SolutionA stream of liquid, set at an angle θ, is directed against a plane surface (figure). The liquid, after hitting the surface, spreads over it. Find the pressure on the surface. The density of the liquid is ρ and its velocity is v.
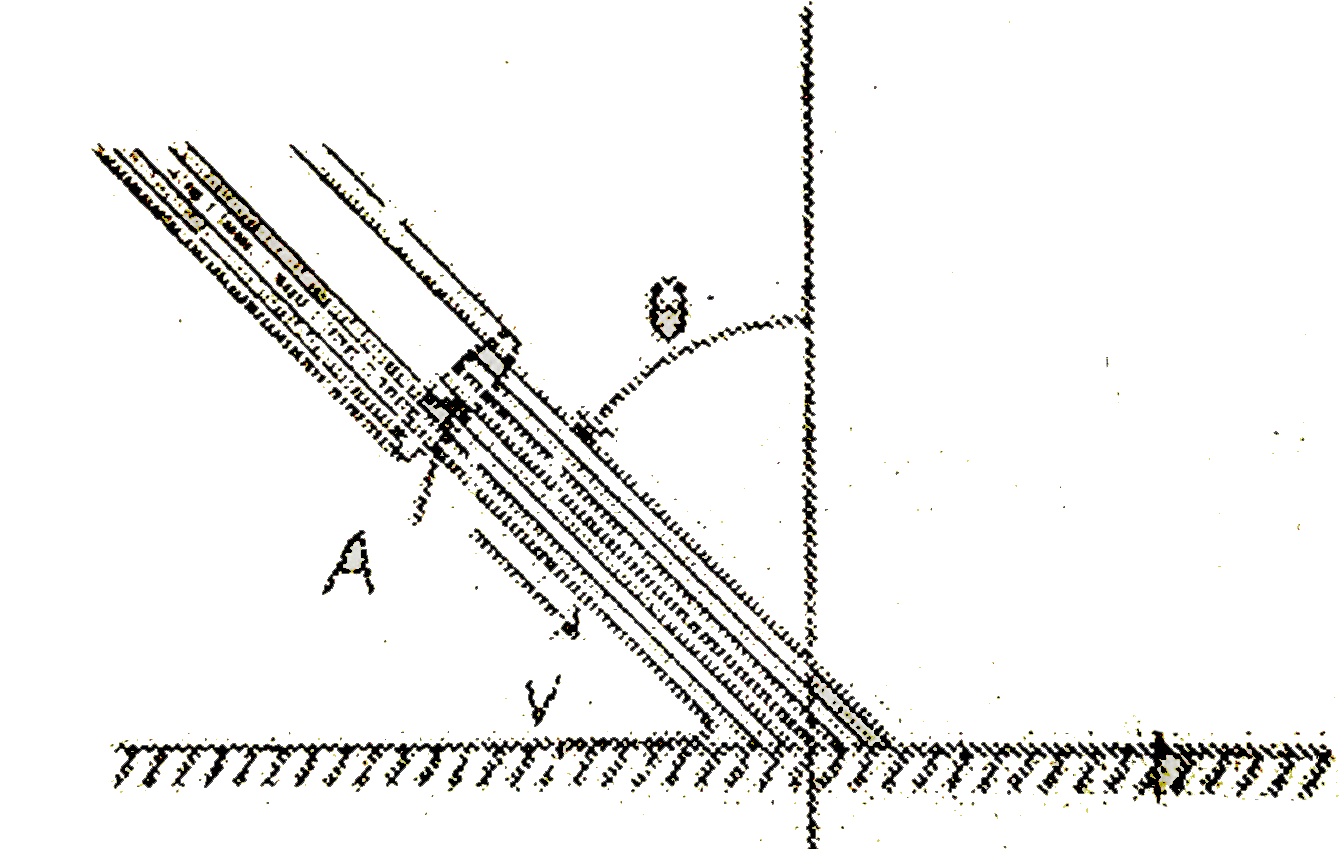
View SolutionSpherical rain drop evaporates at a rate proportional to its surface area. The differential equation corresponding to the rate of change of the radius of the rain drop if the constant of proportionality is K>0 is
View Solution