Two spherical bodies A (radius 6cm) and B (radius 18cm) are at temperature T1 and T2 respectively The maximum intensity in the emission spectrum of A is at 500nm and in that of B is at 1500nm considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of B . ?
The correct Answer is:9
To find the ratio of the rate of total energy radiated by two spherical bodies A and B, we will use Wien's law and Stefan-Boltzmann law.
1. Identify Given Values:
- Radius of body A, RA=6cm
- Radius of body B, RB=18cm
- Wavelength of maximum intensity for A, λA=500nm
- Wavelength of maximum intensity for B, λB=1500nm
2. Use Wien's Displacement Law:
- According to Wien's law, the product of the temperature T and the wavelength λ at which the emission is maximum is constant:
λATA=λBTB
- Rearranging gives us:
TATB=λBλA
- Substituting the values:
TATB=1500nm500nm=3
3. Apply Stefan-Boltzmann Law:
- The power (rate of energy radiated) for a black body is given by:
P=σAT4
- Where σ is the Stefan-Boltzmann constant and A is the surface area.
- For a sphere, the surface area A is given by A=4πR2.
4. Calculate the Ratio of Power:
- The power radiated by A and B can be expressed as:
PA=σ(4πR2A)T4A
PB=σ(4πR2B)T4B
- The ratio PAPB becomes:
PAPB=R2AT4AR2BT4B
5. Substituting Values:
- Substitute RA=6cm and RB=18cm:
PAPB=(6)2T4A(18)2T4B
- This simplifies to:
PAPB=36T4A324T4B=19⋅T4AT4B
6. Using the Temperature Ratio:
- From step 2, we found TATB=3:
T4AT4B=34=81
- Therefore, substituting this back gives:
PAPB=19⋅81=9
Final Answer:
The ratio of the rate of total energy radiated by A to that of B is:
PAPB=9
- Radius of body A, RA=6cm
- Radius of body B, RB=18cm
- Wavelength of maximum intensity for A, λA=500nm
- Wavelength of maximum intensity for B, λB=1500nm
- According to Wien's law, the product of the temperature T and the wavelength λ at which the emission is maximum is constant:
λATA=λBTB
- Rearranging gives us:
TATB=λBλA
- Substituting the values:
TATB=1500nm500nm=3
- The power (rate of energy radiated) for a black body is given by:
P=σAT4
- Where σ is the Stefan-Boltzmann constant and A is the surface area.
- For a sphere, the surface area A is given by A=4πR2.
- The power radiated by A and B can be expressed as:
PA=σ(4πR2A)T4A
PB=σ(4πR2B)T4B
- The ratio PAPB becomes:
PAPB=R2AT4AR2BT4B
- Substitute RA=6cm and RB=18cm:
PAPB=(6)2T4A(18)2T4B
- This simplifies to:
PAPB=36T4A324T4B=19⋅T4AT4B
- From step 2, we found TATB=3:
T4AT4B=34=81
- Therefore, substituting this back gives:
PAPB=19⋅81=9
The ratio of the rate of total energy radiated by A to that of B is:
PAPB=9
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:Level -2
Explore 50 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Main (Archive) Level - 1
Explore 48 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:PHYSICS
Explore 30 Videos
Similar Questions
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionIf the radius of a star is R and it acts as a black body, what would b the temperature of the star, in which the rate of energy production is Q?
View Solution
Knowledge Check
The plots of intensity versus wavelength fro three black bodies at temperatures T1,T2 and T3 respectively and shown in Fig. 15.11.1. Their temperatures are such that
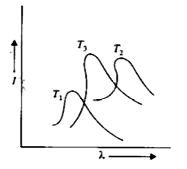 AT1>T2>T3BT1>T3>T2CT2>T3>T1DT3>T2>T1
AT1>T2>T3BT1>T3>T2CT2>T3>T1DT3>T2>T1
If the radius of a star is R and it acts as a black body, what would b the temperature of the star, in which the rate of energy production is Q?
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
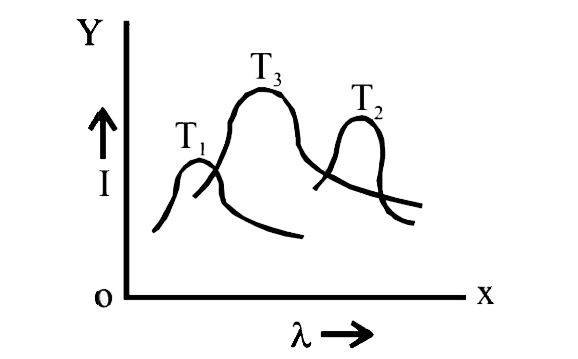
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
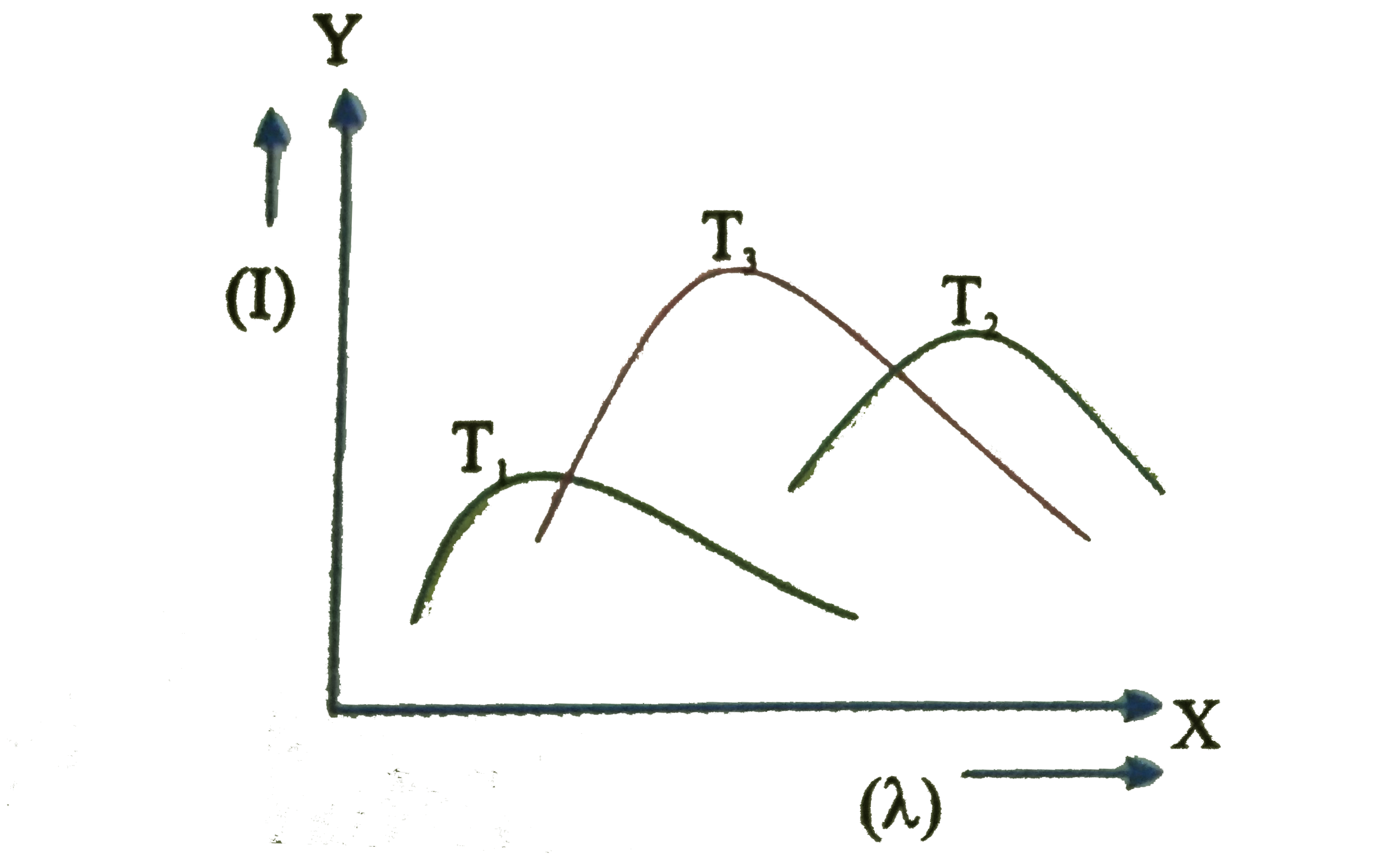
View SolutionThe plots of intensity versus wavelength for three black bodies at temperatures T1,T2 and T3 respectively are shown in Their temperatures are shown in How their temperatures are related ?
 .
.
View SolutionTwo bulbs A and B of equal capacity are filled with He and SO2, respectively, at the same temperature.
(a) If the pressures in the two bulbs are same, what will be the ratio of the velocities of the molecules of the two gases?
View SolutionA system consists of two concentric spherical shells of radii a and b(b>a) maintained at tempareture T1 and T2 respectively.The radial rate of flow of heat through subtance between the two concentric spherical shells is proportional to
View SolutionA heated body maitained at T K emits thermal radiation of total energy E with a maximum intensity at frequency v. The emissivity of the material is 0.5. If the temperature of the body be increased and maintained at temperature 3T K, then :-
(i) The maximum intensity of the emitted radiation will occur at frequency v/3
(ii) The maximum intensity of the emitted radiation will occur at frequency 3v.
(iii) The total energy of emitted radiation will become 81 E
(iv) The total energy of emitted radiation will become 27 E
View Solution