According to Stefan's law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m. When detonated, it reaches temperature of 106K and can be treated as a black body.
(a) Estimate the power it radiates.
(b) If surrounding has water at 30∘C, how much water can 10% of the energy produced evaporate in 1s ?
[Sw=4186.0J/kgKandLv=22.6×105J/g]
(c) If all this energy U is the form of radiation, corresponding momentum is p=U/c. How much momentum per unit time does it impart on unit area at a distance of 1 km?
(i) Radius of the ball,r=0.5m σ=5.67×10−8Wm−2K−4,T=106K
Surface area of nuclear weapon, A=4πr2=4×3.14×(0.5)2=3.14m2
∴ Power radiated , p=(σT4)A=5.67×10−8×(106)4×3.14=1.8×1017W
(ii) Energy radiated , E=P×t
=1.8×1017W×1s=1.8×1017J
Q=10%ofE=1.8×1016J
Also , Q=mCwΔT+mLV=m(CWΔT+LV)
Here CW=4186Jkg−1K−1
LV=22.6×105Jkg−1
ΔT=100−30=70∘C=70K
∴m=Q(CWΔT+LV)=1.8×10164186×70+22.6×105=1.8×101625.53×105=7×109kg
(iii) ∵p=UC
The radiation spread in an area of 4πr2
Here, r=1km=103 m
Momentum imparted per unit time on a unit area at a distance r,
=(U/C)4πr2t=U4πCr2t=4πCr2=1.8×10174×3.14×3×108×106=47.7Nm−2
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -1
90 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -2
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
Which of the following pairs represent of the same physical quantities?
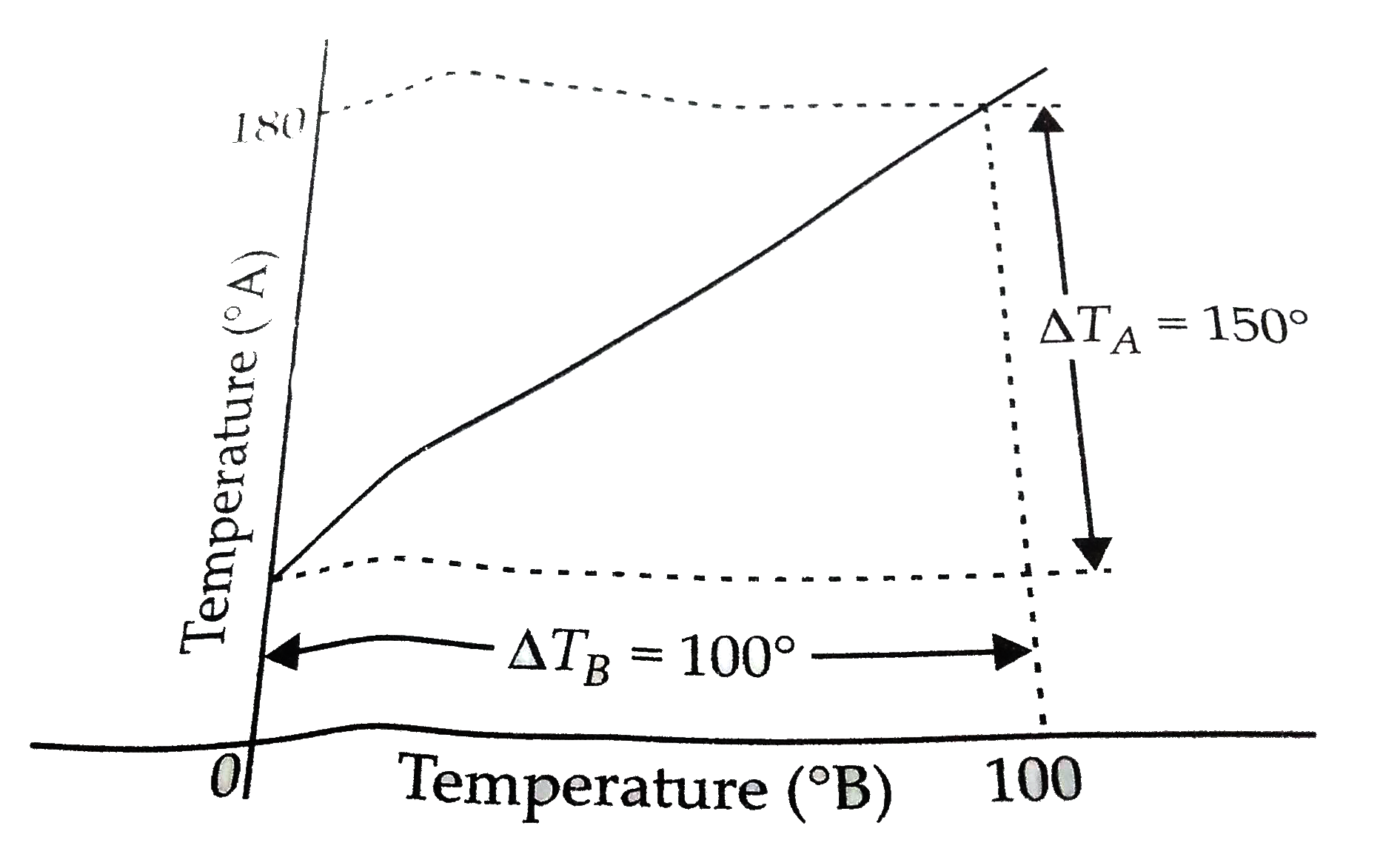
View SolutionThe graph between two temperature scales A and B is shown in figure. Between upper fixed point and lower fixed point there are 150 equal division on scale A and 100 on scale B. The relationship for conversion between the two scales is given by
View SolutionThe angle of dip is the angle
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionAc cording to Stefan' law of radiation, a black body radiates energy sigma T^4 from its unit surface area every second where T is the surface temperature of the black body and sigma = 5.67 xx 10^(-8) W//m^2 K^4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m When detoneted, it reachs temperature of 10^6 K and can be treated as a black body. (a) Estimate the power it radiates. (b) if surrounding has water at 30^@C how much water can 10% of the energy produced evaporate in 1s ? [s_w = 4186.0 J//Kg K and L_(upsilon) = 22.6 xx 10^5 J//kg] (c ) If all this energy U is in the form of radiation, corresponding momentum is p = U//c. How much momentum per unit time does it impart on unit area at a distance of 1 km ?
View SolutionAccording to stefan's law of radiation a black body radiates energy σT4 from is unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's of as a ball of radius 0.5m When detonated it reaches temperature of 106K and can be treated as a black body Estimate the power it radiates .
View SolutionSurface temperature of sun is 6000 K . Considering sun as a perfectly black body, calculate the energy given out by sun per second in radiation. Radius of sun = 6.9 xx 10^(8) m and sigma = 5.67 xx 10^(-8) J s^(-1)m^(-2) K^(-4)
View SolutionA body with surface area (A), temperature (T) and emissivity (e) = 0.6 is kept inside a spherical black body. What will be the maximum energy radiated ? [ sigma is Stefan's constant]
View SolutionA spherical body of emissivity e, placed inside a perfectly black body (emissivity = 1) is maintained at absolute temperature T. The energy radiated by a unit area of the body per second will be (σ is Stefan's constant)
View SolutionThe temperature of a perfect black body is 727^(@)C and its area is 0.1 m^(2) . If Stefan's constant is 5.67 xx 10^(-8) watt//m^(2)-s-K^(4) , then heat radiated by it in 1 minute is:
View SolutionCalculate the temperature at which a perfect black body radiates at the rate of 1 W cm^(-2) , value of Stefan's constant, sigma = 5.67 xx 10^(-5) W m^(-2) K^(-8)
View SolutionCalculate the temperature at which a perfect black body radiates at the rate of 1Wcm−2, value of Stefan's constant,
σ=5.67×10−8Wm−2K−4
View SolutionAccording to Stefan's law of radiation, a black body radiates energy sigmaT^(4) from its unit surface area every second where T is the surface temperature of the black body and sigma=5.67xx10^(-8)W//m^(2)K^(4) is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m. When detonated, it reaches temperature of 10^(6) K and can be treated as a black body. Estimate the power it radiates.
View SolutionAccording to Stefan's law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m. When detonated, it reaches temperature of 106 K and can be treated as a black body.
If surrounding has water at 30∘C, how much water can 10% of the energy produced evaporate in 1 s ?
[Sw=4186.0 J/kg K and Lv=22.6×105 J/kg].
View SolutionAccording to Stefan's law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m. When detonated, it reaches temperature of 106 K and can be treated as a black body.
If all this energy U is in the form of radiation, corresponding momentum is p=Uc. How much momentum per unit time does it impart on unit area at a distance of 1 km ?
View SolutionAc cording to Stefan' law of radiation, a black body radiates energy sigma T^4 from its unit surface area every second where T is the surface temperature of the black body and sigma = 5.67 xx 10^(-8) W//m^2 K^4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m When detoneted, it reachs temperature of 10^6 K and can be treated as a black body. (a) Estimate the power it radiates. (b) if surrounding has water at 30^@C how much water can 10% of the energy produced evaporate in 1s ? [s_w = 4186.0 J//Kg K and L_(upsilon) = 22.6 xx 10^5 J//kg] (c ) If all this energy U is in the form of radiation, corresponding momentum is p = U//c. How much momentum per unit time does it impart on unit area at a distance of 1 km ?
View Solution
