An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be length of the air column above mercury in the tube now? (atmospheric pressure =76 cm of Hg)
38 cm
6 cm
16 cm
22 cm
The correct Answer is:C
When glass tube is open, pressure inside it =P0
When the open end of glass tube is closed, then pressure inside it = P'
P'=P0−ρgx ...(i)
Work done in case I = Work done in case II
Now, P0A(8)=P'A(54−x)
⇒P0(8)=(P0−ρgx)(54−x) [Using(i)]
⇒ρg(76)(8)=ρg(76−x)(54−x)
76(8)=(76−x)(54−x)
On solving x = 38 cm
Therefore, air column = 54−38=16cm
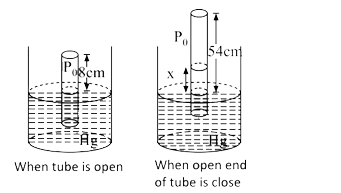
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -250videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be length of the air column above mercury in the tube now? (atmospheric pressure =76 cm of Hg)
View Solution
If above tube is placed vertically with the open and upward then find the length of the air column.View Solution
Knowledge Check
- Question 1 - Select One
A thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of 60∘ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at 30∘C).
A75.4B45.8C67.5D89.3

If the above tube is kept in vertical position by how much length the mercury column descends ?View SolutionA vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
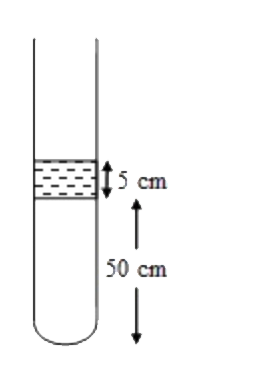 View Solution
View SolutionA uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
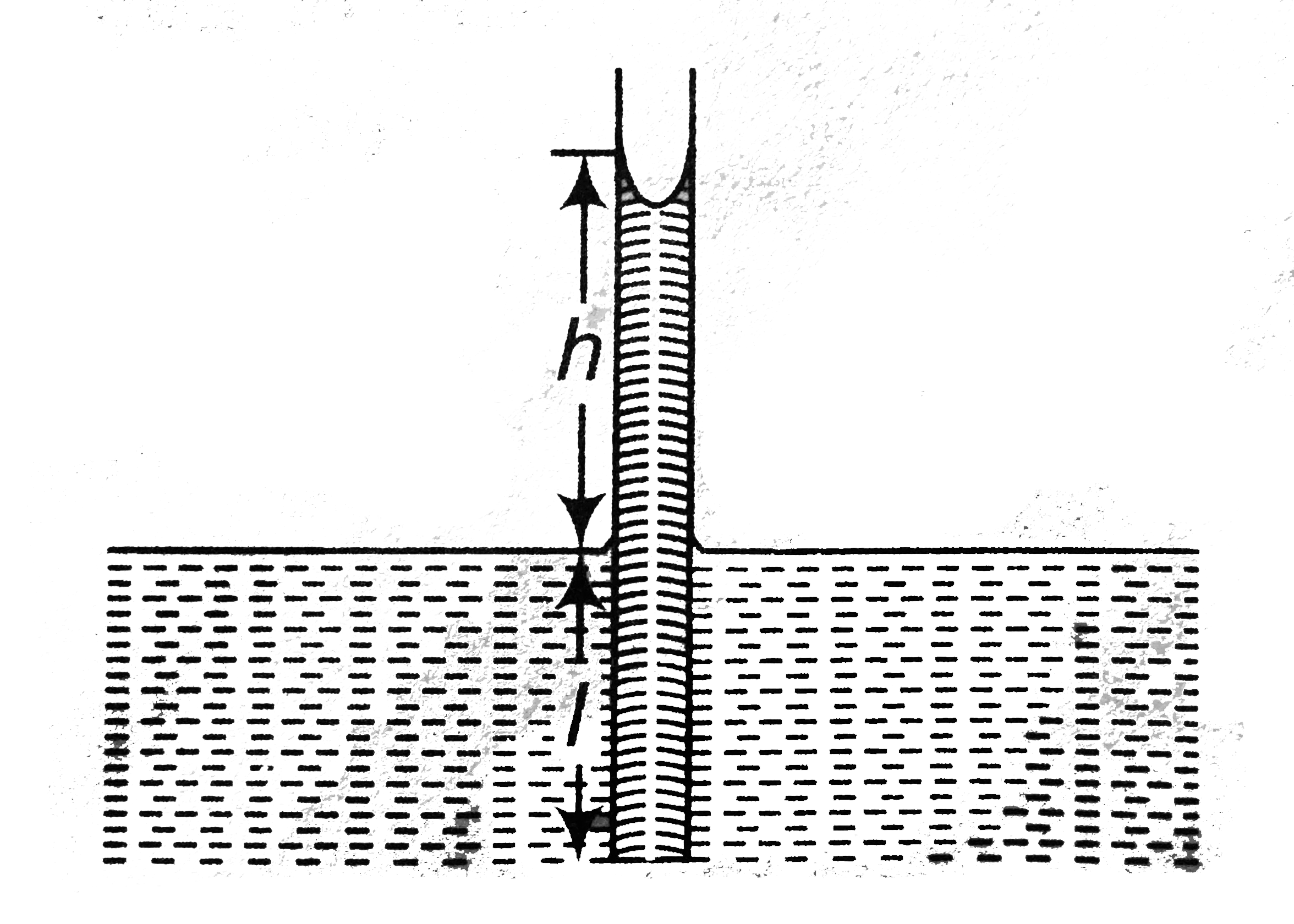 .View Solution
.View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View SolutionA mercury barometer reads 75cm. Now 3cm3 of atmospheric air is introduced into the tube. The mercury falls to a height of 65 cm and the length of air column above the mercury is found to be 15 cm Calculate the cross-sectional area of the barometer tube.
View SolutionA thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of 60∘ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at 30∘C).
View Solution
