Question

State and prove Bernouli's theorem.

Explanation

For the streamline flow of an ideal liquid, the sum of the pressure energy per unit volume, potential energy per unit volume and kinetic energy per unit volume is always constant, whereas an ideal liquid is one which is incompressible and can flow from one place to another without friction.
Proof of Bernoulli’s Theorem :
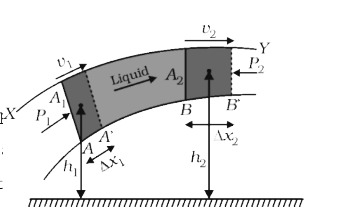
Let us consider a tube XY through which a liquid is having streamline flow as shown in figure.
Let ` P_1 , P_2 ` = pressures at the sections A and B respectively,
` A _ 1, A _ 2 ` = areas of cross-section of tube at A and B respectively,
` h_1 , h _ 2 ` = heights of the cross-section A and B respectively.
As the liquid flows from A to B, ` P_1 gt P_2 `
Since the liquid is incompressible, when it flows from AB to ` A'B' ` (where ` AA' = Delta x _ 1 and BB' = Delta x _ 2 ) ` , Volume of the liquid between ` AA' ` = volume of the liquid between BB' ` = Delta V ` (say ) where
` Delta V = A_1 Delta x _ 1 = A _ 2 Delta x _ 2 `
Further, according to the equation of continuity, ` A _ 1 v _ 1 = A _ 2 v _ 2 , ` since ` A _ 2 lt A _ 1 , v _ 2 gt v_1 `
Thus, the velocity ` (v_2 ) ` at B is more than velocity ` (v_1 )` at A
Force acting on the liquid at the ` A = P_1 A _ 1 `
Work done by the pressure force ` P_1 A _ 1 ` in driving a volume ` Delta V ` through a distance `Delta x _1 `i.e.,
` W_1 = P_1 A _ 1 Delta x _1 = P_1 Delta V (as A_1 Delta x _ 1 = Delta V)`
Similarly, work done by the liquid in driving a volume ` Delta V ` through a distance ` Delta x _ 2` ,i.e.,
` W _2 = P_2 A _ 2 Delta x _ 2 = P _ 2 Delta V (as A _ 1 Delta x _ 2 = Delta V) `
Net work done by the pressure force in driving a volume ` Delta V ` of the liquid i.e.,
` Delta W = W _1 - W _ 2 = P _1 Delta V- P_2 Delta V " " `...(i) Let ` Delta m ` be the mass of the volume ` Delta v ` of the liquid.
since ` h_2 to h_1 ` increase in PE of the liquid , i.e, ` Delta U = (Delta m ) gh _ 2 - (Delta m) gh _1 " " ...(ii) `
Since ` v _ 2 gt v_1 ` , increase in KE of the liquid, i.e, ` Delta K = (1)/(2) (Delta m ) v _ 2 ^ 2 - (1)/(2) (Delta m ) v_1 ^ 2 " " `...(iii)
According to work - energy theorem , `" " Delta W = DeltaU + Delta K " " `...(iv)
From Equations (i), (ii), (iii) and (iv), we get ` P_1 Delta V - P_2 Delta V = ( Delta m ) gh_2 - (Delta m ) gh _1 + (1)/(2) (Delta m) v_2 ^ 2 - (1)/(2) (Delta m ) v_1 ^ 2 `
Dividing both sides by ` Delta V `, We get ` P_1 - P_2 = rho gh _ 2 - rho gh _ 1 + (1)/(2) rho v _ 2 ^ 2 - (1)/(2) rho v _ 1 ^2 `
where ` rho = Delta m// Delta V ` = density of the fluid . thus , ` P_1 + rho gh_1 + (1)/(2) rho v_1 ^ 2 = P_2 + rho gh _ 2 + (1)/(2) rho v _ 2 ^ 2 " " `...(v)
or P + ` rho gh + (1)/(2) rho v ^ 2 ` = constant. this is Bernoulli's theorem.