The position-time relation of a particle moving along the x-axis is given by
x=a−bt+ct2
where a, b and c are positive numbers. The velocity-time graph of the particle is

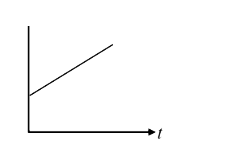
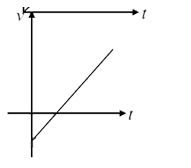
The correct Answer is:C
To find the velocity-time graph of the particle given the position-time relation x=a−bt+ct2, we will follow these steps:
Step 1: Differentiate the position function to find velocity
The velocity v is the first derivative of the position x with respect to time t.
v=dxdt=ddt(a−bt+ct2)
Step 2: Apply the differentiation rules
- The derivative of a constant a is 0.
- The derivative of −bt is −b.
- The derivative of ct2 is 2ct.
Thus, we have:
v=0−b+2ct=−b+2ct
Step 3: Write the velocity equation
The velocity as a function of time t is:
v(t)=−b+2ct
Step 4: Analyze the velocity function
- At t=0:
v(0)=−b+2c(0)=−b
This indicates that the initial velocity is negative since b is a positive number.
- To find when the velocity is zero, set v(t)=0:
0=−b+2ct⟹2ct=b⟹t=b2c
This shows that the velocity becomes zero at a positive time t=b2c.
Step 5: Determine the nature of the velocity-time graph
The equation v(t)=−b+2ct is a linear equation in t with:
- A slope of 2c (which is positive since c is positive).
- A y-intercept of −b (which is negative).
Step 6: Sketch the velocity-time graph
1. The graph starts below the time axis (negative velocity) at t=0.
2. It crosses the time axis at t=b2c (where velocity is zero).
3. After this point, the graph will continue to rise above the time axis (positive velocity) due to the positive slope.
Conclusion
The velocity-time graph is a straight line that starts below the x-axis, crosses it at a positive time, and continues to rise.
The velocity v is the first derivative of the position x with respect to time t.
- The derivative of a constant a is 0.
- The derivative of −bt is −b.
- The derivative of ct2 is 2ct.
The velocity as a function of time t is:
- At t=0:
v(0)=−b+2c(0)=−b
This indicates that the initial velocity is negative since b is a positive number.
0=−b+2ct⟹2ct=b⟹t=b2c
This shows that the velocity becomes zero at a positive time t=b2c.
The equation v(t)=−b+2ct is a linear equation in t with:
- A slope of 2c (which is positive since c is positive).
- A y-intercept of −b (which is negative).
1. The graph starts below the time axis (negative velocity) at t=0.
2. It crosses the time axis at t=b2c (where velocity is zero).
3. After this point, the graph will continue to rise above the time axis (positive velocity) due to the positive slope.
The velocity-time graph is a straight line that starts below the x-axis, crosses it at a positive time, and continues to rise.
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:LEVEL 2
Explore 65 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:JEE MAIN (archive)
Explore 19 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:JEE Advanced (archive)
Explore 14 Videos
- JEE MAIN REVISON TEST-23Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISON TEST-23Exercise:PHYSICS (SECTION 2)
Explore 1 Video
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
Similar Questions
Position of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe position of a particle moving along x- axis is given by x=x0cos2(ωt) . Its when it is at mean position is
View SolutionThe position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
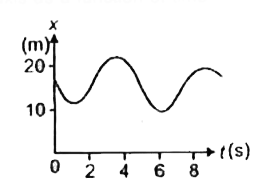
View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
View SolutionThe position x of a particle with respect to time t along the x-axis is given by x=9t2−t3 where x is in meter and t in second. What will be the position of this particle when it achieves maximum speed along the positive x direction
View SolutionThe reation between the time t and position x for a particle moving on x-axis is given by t=px2+qx, where p and q are constants. The relation between velocity v and acceleration a is as
View SolutionFigure shows the position of a particle moving on the X-axis as a function of time.

View SolutionThe linear momentum of a particle as a fuction of time 't' is given by , p = a +bt , where a and b are positive constants . What is the force acting on the particle ?
View Solution