Question

The air column in a pipe closed at one end is made to vibrated in its second overtone by a tuning fork of frequency $440H_Z$ . The speed of sound in air is $330m/s$ . End corrections may be neglected. Let $p_o$ denotes the mean pressure at any point in the pipe, end $\Delta p_o$ the maximum amplitude of pressure variation.
(a) Find the length $L$ of the air column.
(b) What is the amplitude of varitation at the middle of the column ?
(c) What are the maximum and minimum pressures at the open end of the pipe?
(d) What are the maximum and minimum pressure at the closed end of the pipe ?

Options

A. A-R,B-S,C-P,D-S
B. A-R,B-P,C-P,D-S
C. A-R,B-P,C-Q,D-Q
D. A-R,B-P,C-Q,D-S

Answer

C

Explanation

A. The fundamental frequency of the closed organ pipe=`V//4l`. In closed organ pipe only odd harmonics are present.
Second overtone of pipe`=5v//4L`
Given `5v//4L=440`
On solving, we get `L=(5v)/(4xx440)=(5xx330)/(4xx440)=(15)/(16)m=0.9375m=93.75cm`
B. The equation of variation of presure amplitude at any distance x from the node is
`DeltaP=DeltaP_(0)coskx`
Pressure variation is maximum at a node and minimum (zero) at antinode
Distance of centre C from `N_(2)` is `(lamda)/(8)`
`DeltaP=DeltaP_(0)"cos"(2pi)/(lamda)xx(lamda)/(8)=DeltaP_(0)(pi)/(4)=(DeltaP_(0))/(sqrt(2))`

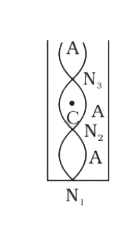
C & D : At antinode, the pressure variation is minimum (zero), therefore at antinode pressure remains equal to
`P_(0)` (Always).
Therefore, at antinode `P_("max")=P_("min")=P_(0)`.