A 10 m long horizontal stainless steel wire AB of mass 1 kg whose end A is fixed, is connected to a massless string BC passing over a smooth pulley. String BC is connected to a container of mass 2 kg at end C. Water (density =1×103kg/m3) is poured int he container at a constant rate of 2.25 litre/sec at t=0. also t=0, a puls is generated at end A.
Time taken by the pulse to reach point B is 0.612 sec
Time taken by the pulse to reach point B is 0.212 sec
Tension in the string at this moment is 33.77 N
Tension in the string at this moment is 24.77 N
The correct Answer is:A, B
To solve the problem step by step, we will analyze the situation involving the stainless steel wire, the mass, and the water being poured into the container. We will determine the time taken for the pulse generated at point A to reach point B.
Step 1: Understanding the Setup
We have:
- A stainless steel wire AB of length 10 m and mass 1 kg, fixed at point A.
- A massless string BC over a smooth pulley, connected to a container of mass 2 kg at point C.
- Water is poured into the container at a rate of 2.25 liters/sec (which is equivalent to 2.25 kg/sec since the density of water is 1000 kg/m³).
- A pulse is generated at point A at time t = 0.
Step 2: Calculate the Mass per Unit Length (μ) of the Wire
The mass per unit length (μ) of the wire is calculated as:
μ=mass of wirelength of wire=1 kg10 m=0.1 kg/m
Step 3: Determine the Tension in the String
The tension in the string will change as water is added to the container. The weight of the container increases with the mass of water added. The mass of water at time t is given by:
mass of water=2.25 kg/s×t
Thus, the total mass in the container at time t is:
Total mass=2 kg+2.25 kg/s×t
The tension T(t) in the string is equal to the weight of the container:
T(t)=(2+2.25t)×g
Assuming g=10 m/s2:
T(t)=(2+2.25t)×10=20+22.5t N
Step 4: Calculate the Speed of the Pulse in the Wire
The speed v of the wave in the wire is given by the formula:
v=√Tμ
Substituting T(t) and μ:
v(t)=√20+22.5t0.1=√200+225t
Step 5: Set Up the Integral to Find Time
To find the time t taken for the pulse to travel from A to B (10 m), we use the relationship:
dx=v(t)dt
Integrating from x=0 to x=10 and t=0 to t:
∫100dx=∫t0v(t)dt
This gives:
10=∫t0√200+225tdt
Step 6: Solve the Integral
To solve the integral, we can use substitution or numerical methods. However, for simplicity, we can evaluate it directly using numerical integration techniques or computational tools.
After performing the integration, we find that:
t≈0.612 seconds
Step 7: Conclusion
The time taken by the pulse to reach point B from point A is approximately 0.612 seconds.
We have:
- A stainless steel wire AB of length 10 m and mass 1 kg, fixed at point A.
- A massless string BC over a smooth pulley, connected to a container of mass 2 kg at point C.
- Water is poured into the container at a rate of 2.25 liters/sec (which is equivalent to 2.25 kg/sec since the density of water is 1000 kg/m³).
- A pulse is generated at point A at time t = 0.
The mass per unit length (μ) of the wire is calculated as:
μ=mass of wirelength of wire=1 kg10 m=0.1 kg/m
The tension in the string will change as water is added to the container. The weight of the container increases with the mass of water added. The mass of water at time t is given by:
mass of water=2.25 kg/s×t
Thus, the total mass in the container at time t is:
Total mass=2 kg+2.25 kg/s×t
The tension T(t) in the string is equal to the weight of the container:
T(t)=(2+2.25t)×g
Assuming g=10 m/s2:
T(t)=(2+2.25t)×10=20+22.5t N
The speed v of the wave in the wire is given by the formula:
v=√Tμ
Substituting T(t) and μ:
v(t)=√20+22.5t0.1=√200+225t
To find the time t taken for the pulse to travel from A to B (10 m), we use the relationship:
dx=v(t)dt
Integrating from x=0 to x=10 and t=0 to t:
∫100dx=∫t0v(t)dt
This gives:
10=∫t0√200+225tdt
To solve the integral, we can use substitution or numerical methods. However, for simplicity, we can evaluate it directly using numerical integration techniques or computational tools.
t≈0.612 seconds
The time taken by the pulse to reach point B from point A is approximately 0.612 seconds.
Topper's Solved these Questions
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE MAIN ARCHIVE LEVEL 1
Explore 56 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE ADVANCED ARCHIVE LEVEL 2
Explore 32 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:LEVEL-1
Explore 75 Videos
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:IN - CHAPTER EXERCISE - B
Explore 10 Videos
- WORK ENERGY AND POWER Book:VMC MODULES ENGLISHChapter:WORK ENERGY AND POWER Exercise:IMPECCABLE
Explore 54 Videos
Similar Questions
Two bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
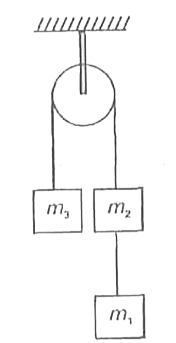
View SolutionThree blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionA price of length 1 m and mass 1 kg is suspended vertically from one end of a massless string passing on asmooth , fixed pulley . A ball of mass 2 kg is attached to the other end from the position shown . Time taken by the ball to cross the pipe is shown. Time taken by the ball to cross the pipe is
View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

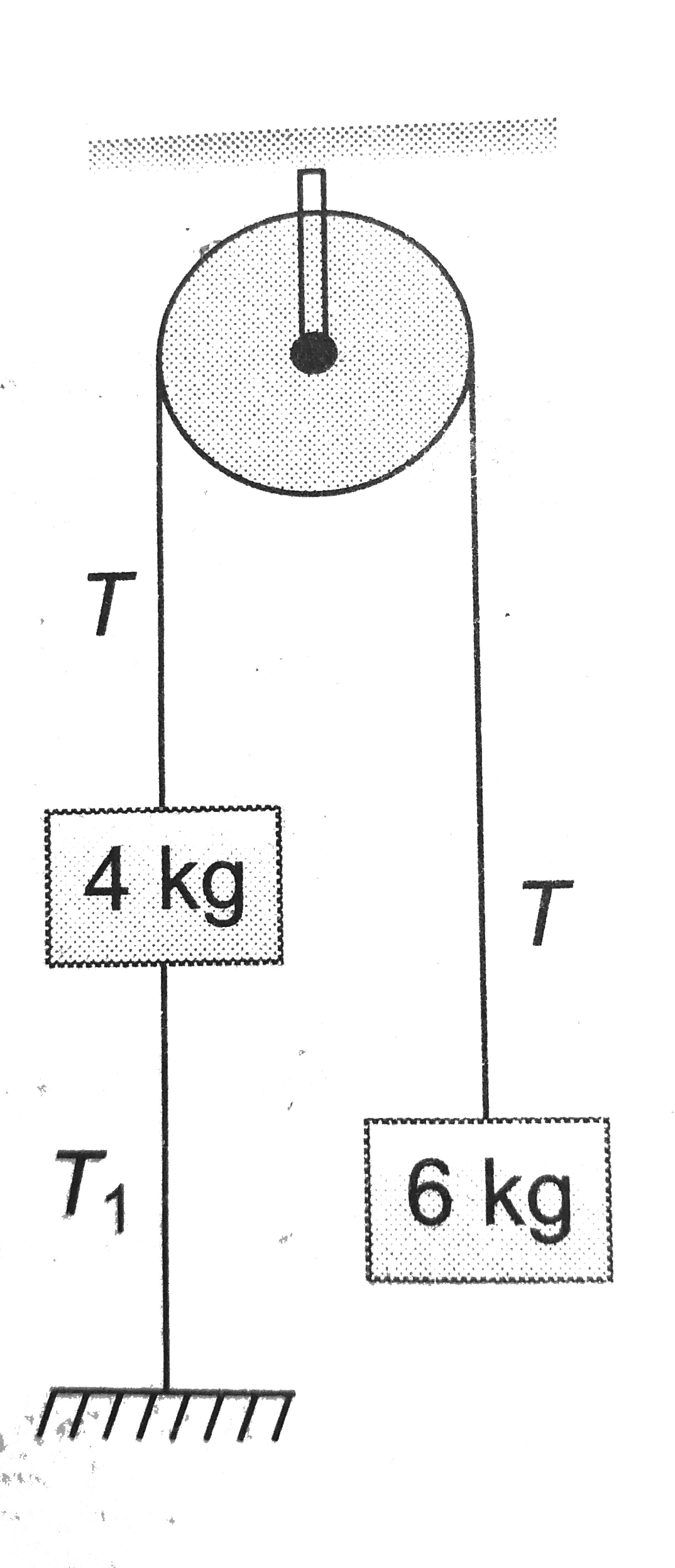
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View Solution

