The density of oxygen is 16 times the density of hydrogen. What is the relation between the speeds of sound in two gases?
To solve the problem of finding the relation between the speeds of sound in oxygen and hydrogen given that the density of oxygen is 16 times the density of hydrogen, we can follow these steps:
1. Define the Densities:
Let the density of hydrogen be ρH. Then, the density of oxygen can be expressed as:
ρO=16ρH
2. Use the Formula for Speed of Sound:
The speed of sound v in a gas is given by the formula:
v=√γPρ
where γ is the adiabatic index (ratio of specific heats), P is the pressure, and ρ is the density of the gas.
3. Write the Speed of Sound for Both Gases:
For hydrogen:
VH=√γPρH
For oxygen:
VO=√γPρO
4. Substitute the Density of Oxygen:
Substitute ρO=16ρH into the equation for VO:
VO=√γP16ρH
5. Find the Ratio of the Speeds:
Now, we can find the ratio of the speeds of sound in oxygen and hydrogen:
VOVH=√γP16ρH√γPρH
6. Simplify the Ratio:
The γP terms will cancel out:
VOVH=√116=14
7. Express the Relation:
Rearranging gives us:
VO=14VH
This means that the speed of sound in oxygen is one-fourth the speed of sound in hydrogen.
Final Relation:
Thus, the relation between the speeds of sound in the two gases is:
VH=4VO
Let the density of hydrogen be ρH. Then, the density of oxygen can be expressed as:
ρO=16ρH
The speed of sound v in a gas is given by the formula:
v=√γPρ
where γ is the adiabatic index (ratio of specific heats), P is the pressure, and ρ is the density of the gas.
For hydrogen:
VH=√γPρH
For oxygen:
VO=√γPρO
Substitute ρO=16ρH into the equation for VO:
VO=√γP16ρH
Now, we can find the ratio of the speeds of sound in oxygen and hydrogen:
VOVH=√γP16ρH√γPρH
The γP terms will cancel out:
VOVH=√116=14
Rearranging gives us:
VO=14VH
This means that the speed of sound in oxygen is one-fourth the speed of sound in hydrogen.
Thus, the relation between the speeds of sound in the two gases is:
VH=4VO
Topper's Solved these Questions
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:LEVEL-1
Explore 75 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:LEVEL-2
Explore 41 Videos
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:IN - CHAPTER EXERCISE - B
Explore 10 Videos
- WORK ENERGY AND POWER Book:VMC MODULES ENGLISHChapter:WORK ENERGY AND POWER Exercise:IMPECCABLE
Explore 54 Videos
Similar Questions
What is the relation between Speed and distance.
View Solutionwhat is the relation between Mass and density.
View SolutionThe density of nucleus is about………….times the density of atom.
View SolutionFind the velocity of sound in O2 at NTP. Given that the velocity of sound in the H2 at NTP is 1880ms−1 the density of oxygen is 16 times the density of hydrogen γ=1.4 for both the gases.
View SolutionHow does the density of gases change with the rise in temperature?
View Solution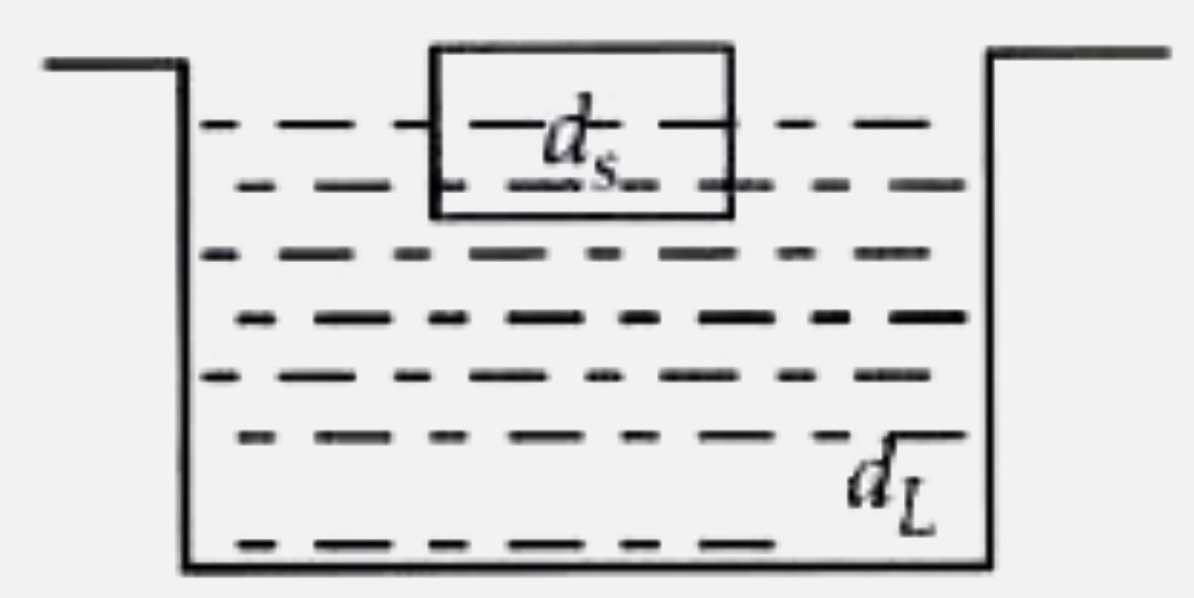
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the relation between dS and dL in the above case?
View SolutionCalculate the speed of sound in oxygen at 273K.
View SolutionThe speed of sound in hydrogen gas at N.T.P is 1328ms−1. If the density of hydrogen is 1/16th of that of air, then the speed of sound in air in at N.T.P is
View SolutionAt a constant temperature what is the relation between pressure P density d of an ideal gas ?
View SolutionCalculate the speed of sound in hydrogen at N.T.P., if density of hydrogen at N.T.P. is 1/16th of air. Given that the speed of sound in air is 332 m/s.
View Solution
