A fixed thermally conducting cylinder has a radius and height . The cylinder is open at its bottom and has a smaller hole at its top. A piston of mass is held at a distance from the top surface, as shown in the figure. The atmospheric pressure is .
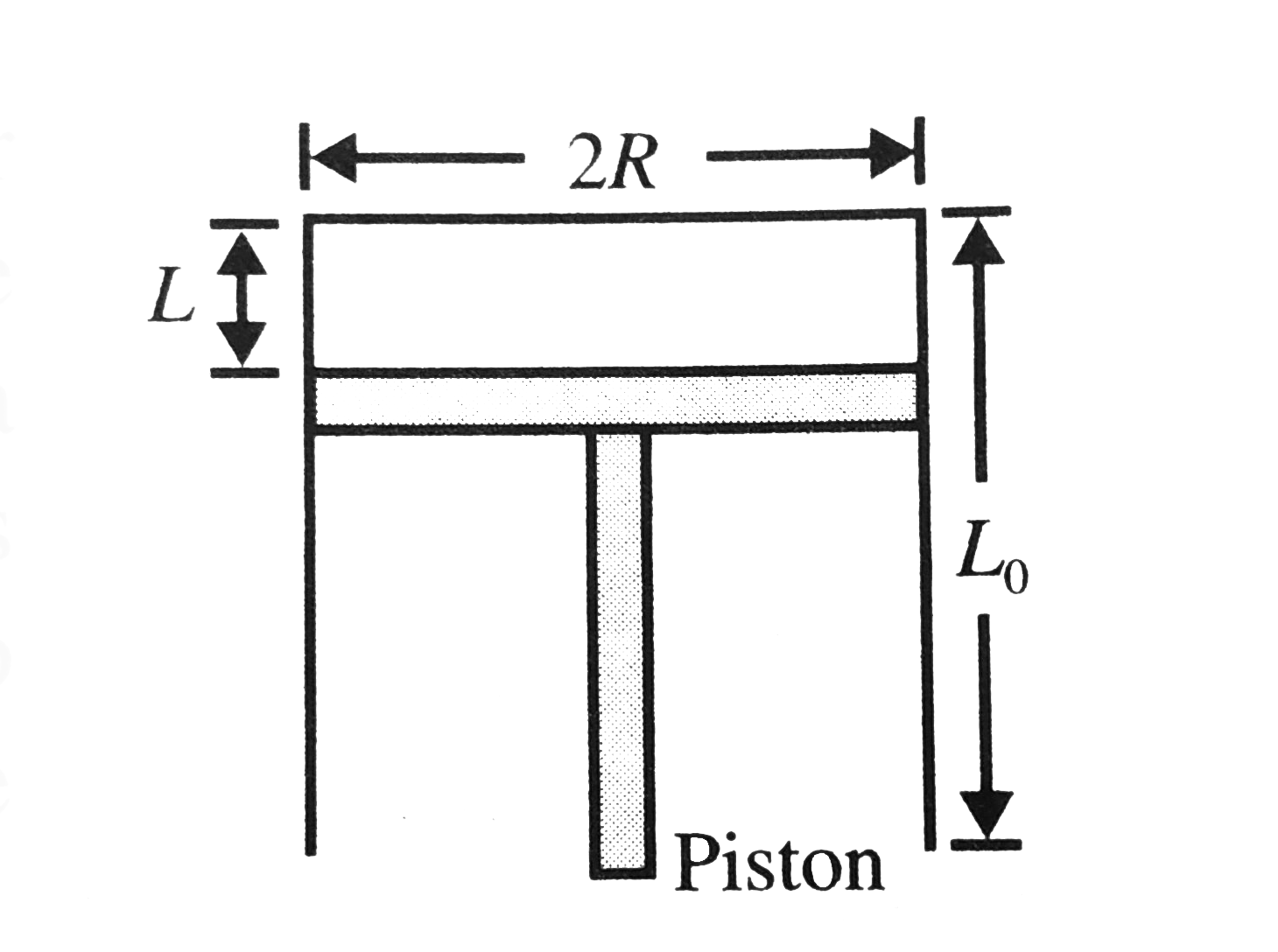
While the piston is at a distance from the top, the hole at the top is sealed. The piston is then released to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
The correct Answer is:D
Let p be the pressure in equilibrium, then
Applying
Therefore, option (D) is correct.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE MAIN (ARCHIVE )81videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
Similar Questions
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at the bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
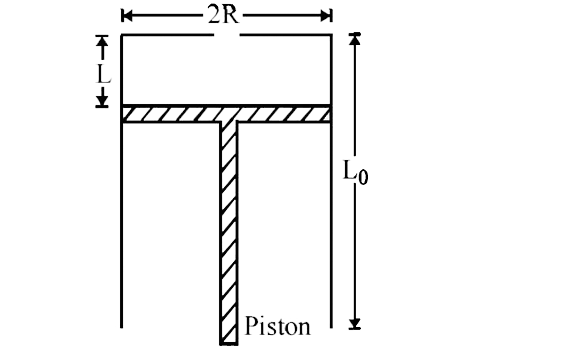
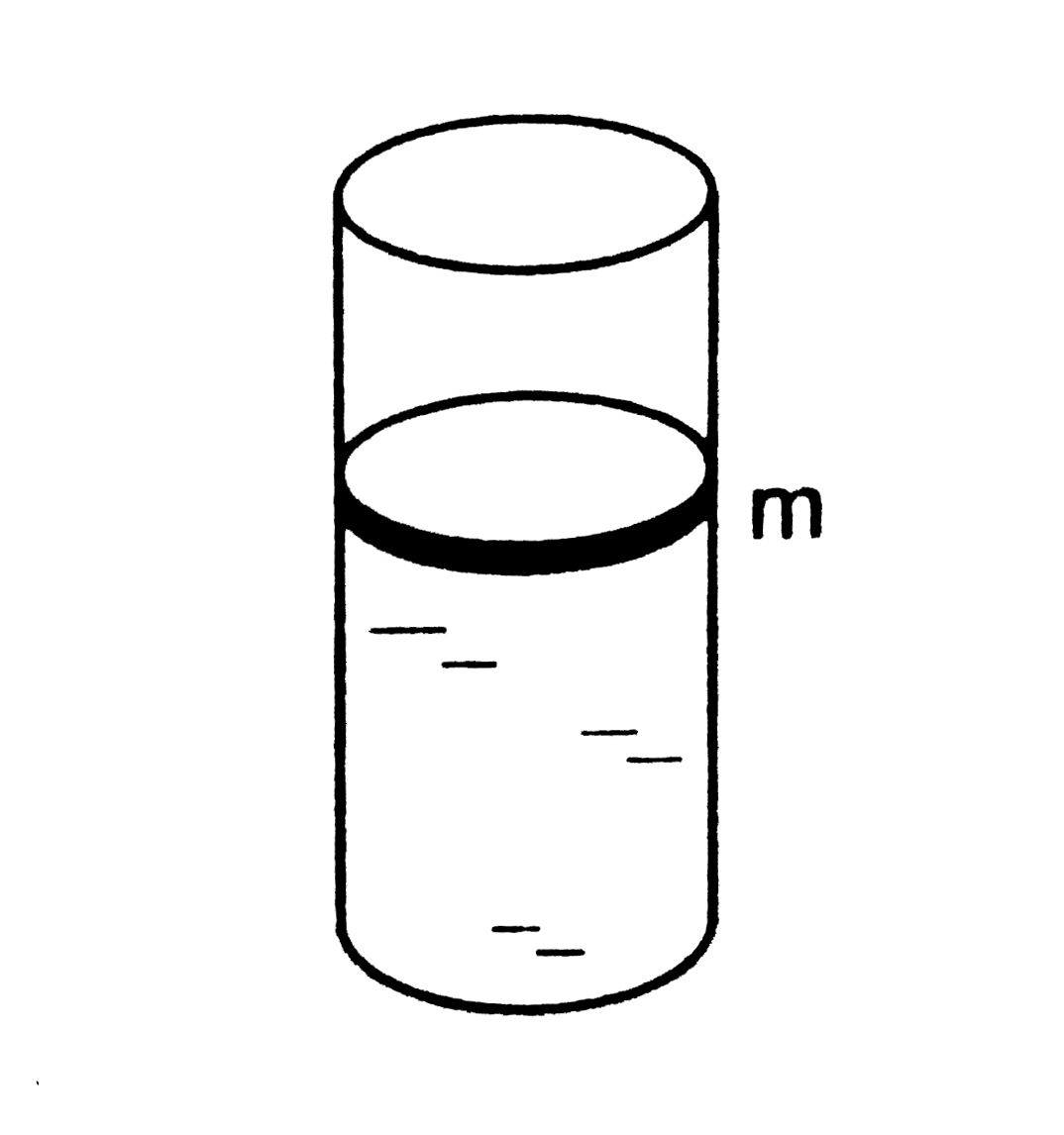
The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then beView SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,View Solution
,View SolutionA light rod of length l is pivoted at distance l/4 from the left end and has two masses m0 and m attached to its ends such that rod is in equilibrium. Find m in terms of m0.
 View Solution
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,View Solution
,View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
 View Solution
View SolutionA cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
View SolutionA very long, solid insulating cylinder with radius R has a cylindrical hole with radius a bored along its entire length. The axis of the hole is at a distance b from the axis of the cylinder, where a<b<R (as shown in figure). The solid material of the cylinder has a uniform volume charge density ρ. Find the magnitude and direction of the electric field inside the hole, and show that this is uniform over the entire hole.
 . View Solution
. View SolutionFrom the top of aspier the angle of depression of the top and bottom of a tower of height h are θ and ϕ respectively. Then height of the spier and its horizontal distance from the tower are respectively.
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is the cross-sectional are of the cylinder. at this time, the temperature of the gas has become.
 View Solution
View Solution


