What happens to the change in internal energy of a gas during adiabatic expansion?
To analyze what happens to the change in internal energy of a gas during adiabatic expansion, we can follow these steps:
1. Understanding Adiabatic Process:
- An adiabatic process is defined as one in which no heat is exchanged between the system (the gas) and its surroundings. This means that the heat transfer Q=0.
2. Applying the First Law of Thermodynamics:
- The first law of thermodynamics states:
ΔU=Q−W
where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
3. Substituting for Adiabatic Conditions:
- Since Q=0 in an adiabatic process, the equation simplifies to:
ΔU=−W
- This indicates that the change in internal energy is equal to the negative of the work done by the gas.
4. Understanding Work Done During Expansion:
- In an adiabatic expansion, the gas does work on the surroundings. Therefore, the work done W is positive.
- As a result, from the equation ΔU=−W, we can conclude that:
ΔU<0
- This means that the internal energy of the gas decreases during adiabatic expansion.
5. Conclusion:
- During adiabatic expansion, the internal energy of the gas decreases because the work done by the gas on the surroundings is positive, leading to a negative change in internal energy.
Summary:
In summary, during adiabatic expansion, the change in internal energy of the gas decreases due to the work done by the gas on its surroundings.
- An adiabatic process is defined as one in which no heat is exchanged between the system (the gas) and its surroundings. This means that the heat transfer Q=0.
- The first law of thermodynamics states:
ΔU=Q−W
where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
- Since Q=0 in an adiabatic process, the equation simplifies to:
ΔU=−W
- This indicates that the change in internal energy is equal to the negative of the work done by the gas.
- In an adiabatic expansion, the gas does work on the surroundings. Therefore, the work done W is positive.
- As a result, from the equation ΔU=−W, we can conclude that:
ΔU<0
- This means that the internal energy of the gas decreases during adiabatic expansion.
- During adiabatic expansion, the internal energy of the gas decreases because the work done by the gas on the surroundings is positive, leading to a negative change in internal energy.
In summary, during adiabatic expansion, the change in internal energy of the gas decreases due to the work done by the gas on its surroundings.
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - level-0 Short Answer Type – II
24 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 1
75 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Video
Similar Questions
The change in internal energy of two moles of a gas during adiabatic expansion is found to be -100 Joule. The work done during the process is
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
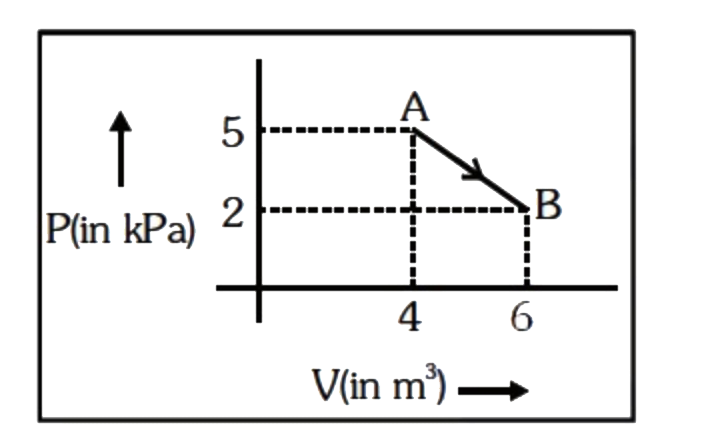
The change in internal energy of the gas during the transition is :
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
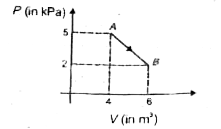
The change to internal energy of the gas during the transition is
View SolutionThe work done and internal energy change during the adiabatic expansion of a gas from a volume of 2.5L to 4.5L against a constant external pressure of 5 atm respectively are (1Latm=101.3J)
View SolutionThe magnitude of ethalphy changes for reversible adiabatic expansion of a gas from volume V1 to V2(in L)is ΔH1 and for irreversible adiabatic expansion for the same expansion is ΔH2. Then
when ΔU1 and ΔU2 are the changes in magnitudes for the internal energy of gas in the two expansions.
View SolutionA gas expands against a variable pressure given by P=20V bar. During expainsion from volume of 1 litre to 10 litre, the gas undergoes a change in internal energy of 400J. Heat absorbed by the gas during expansion ( in KJ):
View SolutionThe change in entropy of an ideal gas during reversible isothermal expansion is
View SolutionWhat happens to the internal energy of a system if work is done by the system?
View SolutionWhat happens to the internal energy of a system if work is done on the system.
View SolutionExpansion of a gas in vacuum is called free expansion. Calculte the work done and the change in internal energy when 1 L of ideal gas expands isothermally into vacuum until its total volume is 5L ?
View Solution

