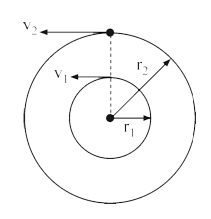
Two satellite $S_{1} and S_{2}$ revolve round a planet in coplanar circular orbits in the same sense. Their periods of revolutions are 1 h nd 8 h respectively. The radius of the orbit of $S_{1}$ is $10^{4} k m$ . When $S_{2}$ is closet to $S_{1}$ ., find (a). The speed of $S_{2}$ relative to $S_{1}$ and (b). the angular speed of $S_{2}$ as observed by an astronaut in $S_{1}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(i)4 (ii

(i) According to Kepler’s third law
$T \propto r^{3 / 2}$
$\frac{T_{1}^{2}}{T_{2}^{2}} = \frac{R_{1}^{3}}{R_{2}^{3}} \Rightarrow R_{2}^{3} = R_{1}^{3} \times \frac{T_{2}^{2}}{T_{1}^{2}} ∴ R_{2}^{3} = 10^{12} \times \frac{8^{2}}{1^{2}} = 64 \times 10^{12} \Rightarrow R_{2} = 4 \times 10^{4}$ km
The speed of satellite $S_{1} V_{1} = \frac{2 π R_{1}}{T_{1}} = \frac{2 π \times 10^{4}}{1}$ km/hr
The speed of satellite $S_{2} V_{2} = \frac{2 π R_{2}}{T_{1}} = \frac{2 π \times 4 \times 10^{4}}{8} = π \times 10^{4}$
The speed of satellites $S_{2}$ relative to $S_{1}$ .

The speed of satellite $S_{2} V_{2} = \frac{2 π R_{2}}{T_{1}} = \frac{2 π \times 4 \times 10^{4}}{8} = π \times 10^{4}$
The speed of satellites $S_{2}$ relative to $S_{1}$ .
$| V_{2.1} | = | V_{2} - V_{1} | = π \times 10^{4} - 2 π \times 10^{4} = π \times 10^{4}$ km/hr
(ii) The angular speed of satellite $S_{2}$ relative to $S_{1}$
$S_{1} = \frac{V_{r}}{R_{r}} = \frac{| V_{2} - V_{1} |}{R_{2} - R_{1}} = \frac{π \times 10^{4}}{(4 \times 10^{4} - 10^{4})} = \frac{π}{3}$ rad/hr

|

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two satellites $S_{1}$ and $S_{2}$ revolve around a planet in coplanar circular orbits in the same sense their periods of revolution are 1 hour and 8hours respectively the radius of the orbit of $S_{1}$ is $10^{4}$ km when $S_{1}$ is closest to $S_{2}$ the angular speed of $S_{2}$ as observed by an astronaut in $S_{1}$ is :
A $π \times 10^{4}$
B $- π \times 10^{4}$
C $π \times 10^{5}$
D $π \times 10^{5}$
Question 2 - Select One
In the above example the angular velocity of $S_{2}$ as actually observed by an astronaut in $S_{1}$ is -
A $3 \times 10^{- 4}$
B $3 \times 10^{23}$
C $3 \times 10^{- 6}$
D $3 \times 10^{- 7}$

VMC MODULES ENGLISH-GRAVITATION-JEE Advance (Archive) NUMERICAL ANSWER

Home
Ask Doubt
Profile