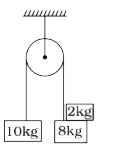
A system is at rest as shown in figure. The tension in the string in . When the 2 kg block is removed, the system moves with some acceleration a and tension in string becomes Find .
The correct Answer is:A

When 2 kg block is removed, acceleration
, ,
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 2
Explore 49 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
Explore 16 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 0 (LONG ANSWER TYPE)
Explore 4 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:IN-CHAPTER EXERCISE-G
Explore 10 Videos
Similar Questions
For the system shown in figure, the tensions in the string
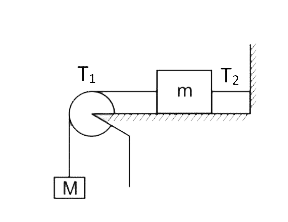
View SolutionThe tension T in the string shown in figure is

View SolutionIn the arrangement shown in figure , find the ratio of tension in the strings attached with 4kg block and the with 1kg block

View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

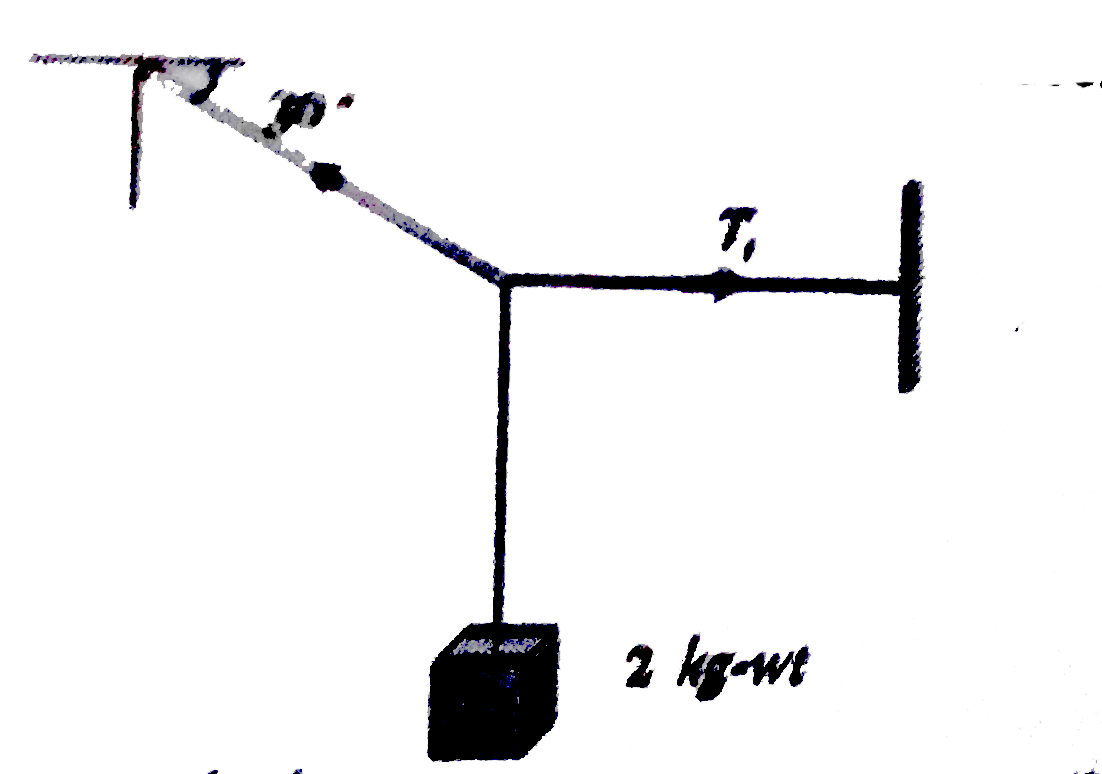
View SolutionA body of weight 2 kg is suspended as shown in the figure. The tensionT1 in the horizontal string (in kg wt ) is
View SolutionFind the tension T2 in the system shown in fig.

View SolutionA body of weight 2 kg is suspended as shown in the figure. The tension T2 in the horizontal string (in kg wt) is :-
View SolutionConsider the situation shown in figure .Both the pulleys and the string and light and all the surfaces are smooth.
(a) Find the acceleration of 1kg block.
(b) Find the tension in the string. (g=10m/s2).

View SolutionFind the tension T2 in the system shown in the figure.
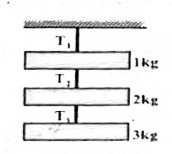
View SolutionIn the arrangment shown in the figure, the ratio of tensions T1:T2:T3 is:

View Solution

