Find (a) the total number and (b) the total mass of protons in 34 mg of NH3 at S.T.P. (Assume the mass of proton =1.6726×10−27kg)
To solve the problem of finding (a) the total number and (b) the total mass of protons in 34 mg of NH₃ at standard temperature and pressure (S.T.P.), we will follow these steps:
Step 1: Convert mass of NH₃ from milligrams to grams
Given:
- Mass of NH₃ = 34 mg
To convert milligrams to grams:
\(
\text{Mass in grams} = \frac{34 \text{ mg}}{1000} = 0.034 \text{ g}
\)
Step 2: Calculate the molar mass of NH₃
The molar mass of NH₃ can be calculated as:
- Nitrogen (N) = 14 g/mol
- Hydrogen (H) = 1 g/mol (there are 3 hydrogen atoms)
Thus, the molar mass of NH₃ is:
\(
\text{Molar mass of } NH₃ = 14 + (3 \times 1) = 17 \text{ g/mol}
\)
Step 3: Calculate the number of moles of NH₃
Using the formula:
\(
\text{Number of moles} (n) = \frac{\text{mass in grams}}{\text{molar mass}}
\)
Substituting the values:
\(
n = \frac{0.034 \text{ g}}{17 \text{ g/mol}} = 2 \times 10^{-3} \text{ moles}
\)
Step 4: Calculate the total number of protons in NH₃
Each molecule of NH₃ contains:
- 1 Nitrogen atom (which has 7 protons)
- 3 Hydrogen atoms (each has 1 proton)
Total number of protons in one molecule of NH₃:
\(
\text{Total protons per molecule} = 7 + 3 = 10 \text{ protons}
\)
Now, to find the total number of protons in 2×10−3 moles of NH₃:
Using Avogadro's number \(N_A = 6.022 \times 10^{23}\):
\(
\text{Total number of protons} = \text{number of moles} \times N_A \times \text{protons per molecule}
\)
Substituting the values:
\(
\text{Total number of protons} = 2 \times 10^{-3} \text{ moles} \times 6.022 \times 10^{23} \text{ molecules/mole} \times 10 \text{ protons/molecule}
\)
Calculating this gives:
\(
\text{Total number of protons} = 1.2044 \times 10^{21} \text{ protons}
\)
Step 5: Calculate the total mass of protons
The mass of one proton is given as \(1.6726 \times 10^{-27} \text{ kg}\).
Total mass of protons:
\(
\text{Total mass of protons} = \text{Total number of protons} \times \text{mass of one proton}
\)
Substituting the values:
\(
\text{Total mass of protons} = 1.2044 \times 10^{21} \text{ protons} \times 1.6726 \times 10^{-27} \text{ kg/proton}
\)
Calculating this gives:
\(
\text{Total mass of protons} \approx 2.0113 \times 10^{-6} \text{ kg} \text{ or } 2.0113 \text{ mg}
\)
Final Answers:
(a) Total number of protons = \(1.2044 \times 10^{21}\) protons
(b) Total mass of protons = \(2.0113 \text{ mg}\)
Given:
- Mass of NH₃ = 34 mg
\(
\text{Mass in grams} = \frac{34 \text{ mg}}{1000} = 0.034 \text{ g}
\)
The molar mass of NH₃ can be calculated as:
- Nitrogen (N) = 14 g/mol
- Hydrogen (H) = 1 g/mol (there are 3 hydrogen atoms)
\(
\text{Molar mass of } NH₃ = 14 + (3 \times 1) = 17 \text{ g/mol}
\)
Using the formula:
\(
\text{Number of moles} (n) = \frac{\text{mass in grams}}{\text{molar mass}}
\)
Substituting the values:
\(
n = \frac{0.034 \text{ g}}{17 \text{ g/mol}} = 2 \times 10^{-3} \text{ moles}
\)
Each molecule of NH₃ contains:
- 1 Nitrogen atom (which has 7 protons)
- 3 Hydrogen atoms (each has 1 proton)
\(
\text{Total protons per molecule} = 7 + 3 = 10 \text{ protons}
\)
Using Avogadro's number \(N_A = 6.022 \times 10^{23}\):
\(
\text{Total number of protons} = \text{number of moles} \times N_A \times \text{protons per molecule}
\)
Substituting the values:
\(
\text{Total number of protons} = 2 \times 10^{-3} \text{ moles} \times 6.022 \times 10^{23} \text{ molecules/mole} \times 10 \text{ protons/molecule}
\)
Calculating this gives:
\(
\text{Total number of protons} = 1.2044 \times 10^{21} \text{ protons}
\)
The mass of one proton is given as \(1.6726 \times 10^{-27} \text{ kg}\).
\(
\text{Total mass of protons} = \text{Total number of protons} \times \text{mass of one proton}
\)
Substituting the values:
\(
\text{Total mass of protons} = 1.2044 \times 10^{21} \text{ protons} \times 1.6726 \times 10^{-27} \text{ kg/proton}
\)
Calculating this gives:
\(
\text{Total mass of protons} \approx 2.0113 \times 10^{-6} \text{ kg} \text{ or } 2.0113 \text{ mg}
\)
(a) Total number of protons = \(1.2044 \times 10^{21}\) protons
(b) Total mass of protons = \(2.0113 \text{ mg}\)
Topper's Solved these Questions
- ATOMIC STRUCTUREBook:VMC MODULES ENGLISHChapter:ATOMIC STRUCTUREExercise:LEVEL - 1
Explore 75 Videos
- ATOMIC STRUCTUREBook:VMC MODULES ENGLISHChapter:ATOMIC STRUCTUREExercise:LEVEL - 2
Explore 50 Videos
- ATOMIC STRUCTUREBook:VMC MODULES ENGLISHChapter:ATOMIC STRUCTUREExercise:Level - 0 (Short Answer Type-II (3 Marks))
Explore 6 Videos
- AMINESBook:VMC MODULES ENGLISHChapter:AMINESExercise:IN CHAPTER EXERCISE H
Explore 10 Videos
- CHEMICAL BONDING & CHEMICAL STRUCTURE Book:VMC MODULES ENGLISHChapter:CHEMICAL BONDING & CHEMICAL STRUCTURE Exercise:IMPECCABLE
Explore 50 Videos
Similar Questions
(i) Calculate the total number of electrons present in 1 mole of methane .
(ii) Find (a) the total number and (b) the total mass of neutrons in 7 mg of .14C. (Assume that mass of a neutron =1.675×10−27g)
(iii) Find (a) the total number of protons and (b) the total mass of protons in 32mg of NH3 at STP. ( mass of proton =1.672×10−27g)
Will the answer change if the temperature and pressure are changed ?
View SolutionFind (a) the total number and (b) the total mass of neutrons in 7 mg of .C14
(Assume that the mass of neutron =1.675×10−27kg)
View Solution
Knowledge Check
Total number of atoms present in 34 g of NH3 is
A4×1023B4.8×1021C2×1023D48×1023
Mass of 112cm3 of NH3 gas at S.T.P. is
View SolutionA proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton=1.6X10−27kg.
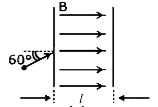
View SolutionThe figure shows a region of length ‘l’ with a uniform magnetic field of 0.3 T in it and a proton entering the region with velocity 4×105 ms−1 making an angle 60∘ with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘l’ is close to (mass of proton =1.67×10−27 kg , charge of the proton =1.6×10−19 C )
View SolutionAssuming the radius of a nucleus to be equal to R=1.3A1/3×10−15m. Where A is its mass number, evaluate the density of nuclei and the number of nucleons per unit volume of the nucleus. Take mass of one nucleon =1.67×10−27kg
View SolutionAssume that a neutron breaks into a proton and an electron . The energy reased during this process is (mass of neutron =1.6725×10−27kg mass of proton =1.6725×10−27kg mass of electron =9×10−31kg)
View SolutionWhen would the wavelength associated with an electron become equal to that with proton ? (Mass of electron =9.10×10−31kg, Mass of proton =1.6725×10−27kg)
View SolutionCalculate the wavelength (in nanometer) associated with a proton moving at 1.0×103ms−1 (Mass of proton =1.67×10−27kgandh=6.63×10−34Js)
View Solution

